题目内容
如图,AB是⊙O的直径,C为圆周上的一点,过点C的直线MN满足∠MCA=∠CBA.
(1)求证:直线MN是⊙O的切线
(2)过点A作AD⊥MN于点D,交⊙O于点E,已知AB=6,BC=3,求阴影部分的面积.

证明:(1)连接OC,∵AB是⊙O的直径,C 为圆周上的一点,
为圆周上的一点,
∴∠ACB=90°,即∠ACO+∠OCB=90°,
∵OC=OB,∴∠OCB=∠OBC,
又∠MCA=∠ABC,故∠MCA= ∠OCB,
∠OCB,
∴∠ACO+∠MCA=90°,即OC⊥MN,直线MN过点C,
∴直线MN是⊙O的切线.(5分)
(2)连接OE、CE,由(1)OC⊥MN,AD⊥MN,得OC∥AE,
在Rt△ACB中,co sB=
sB=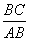 =
=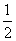 ,∴∠B=60°,故OC=OB=BC=3,
,∴∠B=60°,故OC=OB=BC=3,
∴∠EAO=∠COB=60°,故OE=OA=EA=3,∠EOC=60°,
∴OC=AE,四边形AOCE是平行四边形,故S△EAC=S△EOC(8分)
于是,S阴=S△ADC-S扇形EOC,
在Rt△ACB中,BC=3,AB=6,∴AC=3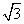 ,
,
在Rt △ADC中,AC=3
△ADC中,AC=3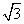 ,∠DCA=∠B=60°,
,∠DCA=∠B=60°,
∴DC=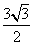 ,AD=
,AD=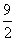 , ∴S△ADC=
, ∴S△ADC=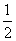 AD·DC=
AD·DC=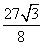 ,(10分)
,(10分)
而S扇形EOC=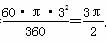 于是S阴=S△ADC-S扇形EOC=
于是S阴=S△ADC-S扇形EOC=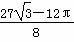

练习册系列答案
相关题目
 =
= 的解为( )
的解为( ) C.-
C.- 1 D.无解
1 D.无解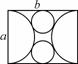
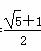 a C.b=
a C.b=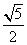 a D. b=
a D. b= a
a  2)·180°.
2)·180°. A.5 B.6 C.11 D.16
A.5 B.6 C.11 D.16 图,那么他所画的三视图中的俯视图应该是( )
图,那么他所画的三视图中的俯视图应该是( )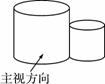
 平均煤耗继续降低,仅为330 000毫克/千瓦时,用科学记数法表示并保留三个有效数字为________毫克/千瓦时.
平均煤耗继续降低,仅为330 000毫克/千瓦时,用科学记数法表示并保留三个有效数字为________毫克/千瓦时.