题目内容
(1)解方程:(3y+1)2=2
(2)根据图象所示化简:a,b为实数,试化简:

解:(1)(3y+1)2=25
3y+1=±5,
当3y+1=5时,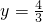
当3y+1=-5时,y=-2
(2)根据数轴可以得到:a<0<b,
∴a-b<0
∴
=a-b-a
=-b
分析:(1)首先利用平方根的定义求得3y+1的值,然后解一元一次方程求的x的值;
(2)首先根据数轴确定a,b的大小和符号,然后根据绝对值的性质以及二次根式的性质即可化简.
点评:考查了实数与数轴、平方根和二次根式的性质与化简解答此题,要弄清以下问题:
①定义:一般地,形如 (a≥0)的代数式叫做二次根式.当a>0时,
(a≥0)的代数式叫做二次根式.当a>0时, 表示a的算术平方根;当a=0时,
表示a的算术平方根;当a=0时, =0;当a<0时,非二次根式(在一元二次方程中,若根号下为负数,则无实数根).
=0;当a<0时,非二次根式(在一元二次方程中,若根号下为负数,则无实数根).
②性质: =|a|.
=|a|.
3y+1=±5,
当3y+1=5时,
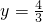
当3y+1=-5时,y=-2
(2)根据数轴可以得到:a<0<b,
∴a-b<0
∴

=a-b-a
=-b
分析:(1)首先利用平方根的定义求得3y+1的值,然后解一元一次方程求的x的值;
(2)首先根据数轴确定a,b的大小和符号,然后根据绝对值的性质以及二次根式的性质即可化简.
点评:考查了实数与数轴、平方根和二次根式的性质与化简解答此题,要弄清以下问题:
①定义:一般地,形如
 (a≥0)的代数式叫做二次根式.当a>0时,
(a≥0)的代数式叫做二次根式.当a>0时, 表示a的算术平方根;当a=0时,
表示a的算术平方根;当a=0时, =0;当a<0时,非二次根式(在一元二次方程中,若根号下为负数,则无实数根).
=0;当a<0时,非二次根式(在一元二次方程中,若根号下为负数,则无实数根).②性质:
 =|a|.
=|a|. 
练习册系列答案
相关题目
 (1)解方程:(3y+1)2=25
(1)解方程:(3y+1)2=25