Question

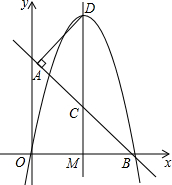如图，直线AB交x轴于点B，交y轴于点A（0，4），直线DM⊥x轴正半轴于点M，交线段AB于点C，DM=6，连接DA，∠DAC=90°，AD：AB=1：2．
（1）求点D的坐标；
（2）求经过O、D、B三点的抛物线的函数关系式．

Answer 1

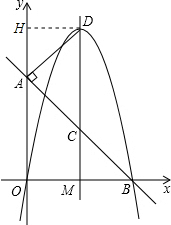解：（1）如图，过点D作DH⊥OA于H．
则∠DHA=∠AOB=90°．
又∵∠DAC=90°，
∴∠HDA=∠OAB（同角的余角相等），
∴△ADH∽△BAO，
∴=．
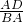又∵AD：AB=1：2，A（0，4），
∴=，
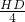则HD=2，
又∵DM=6，
∴D（2，6）；

（2）由（1）知，D（2，6）．
如图，又∵A（0，4），OH=DM=6，
∴HD=HA=2，
∴△HDA是等腰直角三角形，
∴△AOB也是等腰直角三角形，
∴OA=OB=4，
∴B（4，0）．
由抛物线过O（0，0），B（4，0）两点，设抛物线解析式为y=ax（x-4）（a≠0），
将D（2，6）代入，得a=-1.5，所以，抛物线解析式为y=-1.5x（x-4）（或y=-1.5x²+6x）．
分析：（1）如图，过点D作DH⊥OA于H．构建相似三角形：△ADH∽△BAO，由相似三角形对应边成比例求得HD=2，所以D（2，6）；
（2）此题已知抛物线与x轴交于点O、B，所以可以设交点式方程y=ax（x-4）（a≠0），然后把点D的坐标代入来求a的值．
点评：本题考查了二次函数的综合运用．其中涉及到的知识点有待定系数法求二次函数解析式，相似三角形的判定与性质等．此题难度较大，关键是根据△ABO的形状来求得点B的坐标．