题目内容
 在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则能反映y与x之间关系的图象为
在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则能反映y与x之间关系的图象为
- A.

- B.
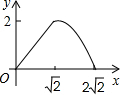
- C.

- D.
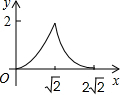
C
分析:分析,EF与X的关系,他们的关系分两种情况,依情况来判断抛物线的开口方向.
解答:∵四边形ABCD是正方形,
∴AC=BD=2 ,OB=OD=
,OB=OD= BD=
BD= ,
,
①当P在OB上时,即0≤x≤ ,
,
∵EF∥AC,
∴△BEF∽△BAC,
∴EF:AC=BP:OB,
∴EF=2BP=2x,
∴y= EF•BP=
EF•BP= ×2x×x=x2;
×2x×x=x2;
②当x在OD上时,即 <x≤2
<x≤2 ,
,
∵EF∥AC,
∴△DEF∽△DAC,
∴EF:AC=DP:OD,
即EF:2 =(2
=(2 -x):
-x): ,
,
∴EF=2(2 -x),
-x),
∴y= EF•BP=
EF•BP= ×2(2
×2(2 -x)×x=-x2+
-x)×x=-x2+ x,
x,
这是一个二次函数,根据二次函数的性质可知:
二次函数的图象是一条抛物线,开口方向决定,二次项的系数.
当系数>0时,抛物线开口向上;系数<0时,开口向下.所以由此图我们会发现,EF的取值,最大是AC.当在AC的左边时,EF=2BP;所以此抛物线开口向上,当在AC的右边时,抛物线就开口向下了.故选C.
点评:此题的关键是利用三角形的面积公式列出二次函数解析式解决问题.
分析:分析,EF与X的关系,他们的关系分两种情况,依情况来判断抛物线的开口方向.
解答:∵四边形ABCD是正方形,
∴AC=BD=2
 ,OB=OD=
,OB=OD= BD=
BD= ,
,①当P在OB上时,即0≤x≤
 ,
,∵EF∥AC,
∴△BEF∽△BAC,
∴EF:AC=BP:OB,
∴EF=2BP=2x,
∴y=
 EF•BP=
EF•BP= ×2x×x=x2;
×2x×x=x2;②当x在OD上时,即
 <x≤2
<x≤2 ,
,∵EF∥AC,
∴△DEF∽△DAC,
∴EF:AC=DP:OD,
即EF:2
 =(2
=(2 -x):
-x): ,
,∴EF=2(2
 -x),
-x),∴y=
 EF•BP=
EF•BP= ×2(2
×2(2 -x)×x=-x2+
-x)×x=-x2+ x,
x,这是一个二次函数,根据二次函数的性质可知:
二次函数的图象是一条抛物线,开口方向决定,二次项的系数.
当系数>0时,抛物线开口向上;系数<0时,开口向下.所以由此图我们会发现,EF的取值,最大是AC.当在AC的左边时,EF=2BP;所以此抛物线开口向上,当在AC的右边时,抛物线就开口向下了.故选C.
点评:此题的关键是利用三角形的面积公式列出二次函数解析式解决问题.

练习册系列答案
相关题目
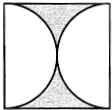 如图,在边长为a的正方形铁块中,以两对边中点为圆心,以a为直径截取两个半圆,求余下废料的面积是多少?
如图,在边长为a的正方形铁块中,以两对边中点为圆心,以a为直径截取两个半圆,求余下废料的面积是多少?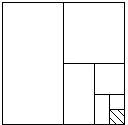 我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
我国著名的数学家华罗庚曾说过:“数形结合百般好,割裂分家万事非”,如图,在边长为1的正方形纸板上,依次贴上面积为
 在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.
在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个无盖的长方体.