题目内容
已知一斜坡的坡比为1:2,斜坡长为15米,则斜坡上最高点离地面的高度为( )
| A、7.5米 | ||||
B、
| ||||
C、3
| ||||
D、6
|
分析:已知斜坡的坡比就是告诉了两直角边的关系,设最高点离地面的高度为x,由勾股定理建立方程,解方程即可.
解答:解:由已知得斜坡垂直高度与水平宽度之比为1:2.
设斜坡上最高点离地面的高度(即垂直高度)为x米,则水平宽度为2x米,
由勾股定理得x2+(2x)2=152,
解之得x=3
.
故选C.
设斜坡上最高点离地面的高度(即垂直高度)为x米,则水平宽度为2x米,
由勾股定理得x2+(2x)2=152,
解之得x=3
| 5 |
故选C.
点评:学会把实际问题转化为解直角三角形的问题.理解坡比的定义.

练习册系列答案
相关题目
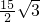 米
米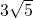 米
米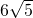 米
米