题目内容
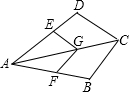
 如图,D是AB边上一点,E是AC上一点,AB=9,AC=6,AD=3.若要使△ADE与△ABC相似,则AE的长为
如图,D是AB边上一点,E是AC上一点,AB=9,AC=6,AD=3.若要使△ADE与△ABC相似,则AE的长为
- A.2
- B.

- C.

- D.2或

D
分析:根据题意,△ADE与△ABC相似,由于题中没有指明对应边,故应该分两种情况讨论求解.
解答:①当△ADE∽△ABC时,有AD:AE=AB:AC,
∵AB=9,AC=6,AD=3,
∴AE=2;
②当△AED∽△ABC时,有AD:AE=AC:AB,
∵AB=6,AC=4,AD=2,
∴AE= ,
,
所以AE等于2或 .
.
故选D.
点评:本题考查了相似三角形的判定和性质,同时考查学生对相似三角形的性质的掌握情况,注意分类讨论思想的运用.
分析:根据题意,△ADE与△ABC相似,由于题中没有指明对应边,故应该分两种情况讨论求解.
解答:①当△ADE∽△ABC时,有AD:AE=AB:AC,
∵AB=9,AC=6,AD=3,
∴AE=2;
②当△AED∽△ABC时,有AD:AE=AC:AB,
∵AB=6,AC=4,AD=2,
∴AE=
 ,
,所以AE等于2或
 .
.故选D.
点评:本题考查了相似三角形的判定和性质,同时考查学生对相似三角形的性质的掌握情况,注意分类讨论思想的运用.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
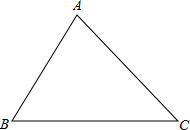
 如图,D是△ABC中BC边上的一点,AB=12,BC=8,BD=5.
如图,D是△ABC中BC边上的一点,AB=12,BC=8,BD=5.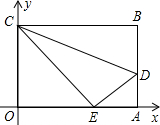 上的点E处.
上的点E处.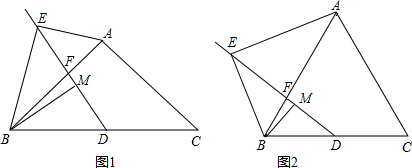
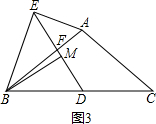
 (2013•南岗区一模)如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若BC=100,则折痕DE的长度是( )
(2013•南岗区一模)如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若BC=100,则折痕DE的长度是( )