Question

直角三角形中，一个锐角为30°，斜边与较小边的和为12cm；则斜边长为

8

cm，这个三角形的面积为

8

3

cm²．

Answer 1

分析：作出图形，根据直角三角形30°角所对的直角边等于斜边的一半可得AB=2AC，再根据AB+AC=12计算即可得解；
利用勾股定理列式求出BC，再根据三角形的面积公式列式计算即可得解．

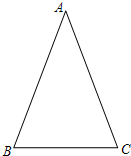
解答：解：如图，∵Rt△ABC的∠B=30°，
∴AB=2AC，
∵AB+AC=12，
∴2AC+AC=12，
解得AC=4cm，
AB=2×4=8cm；

由勾股定理得，BC=

AB2-AC2

=

82-42

=4

3

cm，
∴三角形的面积=

1

2

×4×4

3

=8

3

cm²．
故答案为：8；8

3

．

点评：本题考查了直角三角形30°角所对的直角边等于斜边的一半，勾股定理的应用，熟记性质是解题的关键，作出图形更形象直观．