题目内容
2.已知一元二次方程x2+x-1=0,下列判断正确的是( )| A. | 该方程有两个相等的实数根 | B. | 该方程有一个根为1 | ||
| C. | 该方程没有实数根 | D. | 该方程有一个根为负数 |
分析 根据方程的系数结合根的判别式,可得出△=5>0,从而可得出该方程有两个不相等的实数根,设方程x2+x-1=0的两个实数根分别为a、b,由根与系数的关系可得出ab=-1,由此可得出该方程有一个根为负数,此题得解.
解答 解:∵在方程x2+x-1=0中,△=(-1)2-4×1×(-1)=5>0,
∴方程x2+x-1=0有两个不相等的实数根.
设方程x2+x-1=0的两个实数根分别为a、b,
由根与系数的关系得:ab=-1,
∴该方程有一个根为负数.
故选D.
点评 本题考查了根的判别式以及根与系数的关系,由两根之积为负,找出方程有一个根为负数是解题的关键.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
13.下列计算正确的是( )
| A. | a3+a2=2a5 | B. | a6÷a2=a3 | C. | (a-b)2=a2-b2 | D. | (-2a3)2=4a6 |
17.4的算术平方根是( )
| A. | 2 | B. | 16 | C. | ±2 | D. | ±16 |
7.继短信、QQ之后,微信逐步成为我国手机用户的最爱和移动通信新的增长点,目前,中国移动微信用户数已超过400000000.用科学记数法表示这个数应为( )
| A. | 4×108 | B. | 4×107 | C. | 0.4×108 | D. | 40×107 |
14.德国联邦食品和农业部2016年11月12日通报称,欧洲多国正经历一轮H5N8高致病禽流感疫情,禽流感病毒的形状一般为球形,直径大约为0.000 000 102m,数据0.000 000 102可用科学记数法表示为( )
| A. | 1.02×10-7 | B. | 1.02×10-8 | C. | 1.02×10-9 | D. | 1.02×10-10 |
11.若x=(-2)×(-3),则x的倒数是( )
| A. | $\frac{1}{6}$ | B. | -$\frac{1}{6}$ | C. | -6 | D. | 6 |
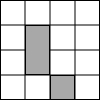 如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形,这样的白色小正方格有( )
如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形,这样的白色小正方格有( ) 如图,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A、B、C和点D、E、F,若AB:AC=1:3,DE=3,则EF的长为( )
如图,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A、B、C和点D、E、F,若AB:AC=1:3,DE=3,则EF的长为( ) 如图,码头A、B分别在海岛O的北偏东45°和北偏东60°方向上,仓库C在海岛O的北偏东75°方向上,码头A、B均在仓库C的正西方向,码头B和仓库C的距离BC=50km,若将一批物资从仓库C用汽车运送到A、B两个码头中的一处,再用货船运送到海岛O,若汽车的行驶速度为50km/h,货船航行的速度为25km/h,问这批物资在哪个码头装船,最早运抵海岛O?(两个码头物资装船所用的时间相同,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,码头A、B分别在海岛O的北偏东45°和北偏东60°方向上,仓库C在海岛O的北偏东75°方向上,码头A、B均在仓库C的正西方向,码头B和仓库C的距离BC=50km,若将一批物资从仓库C用汽车运送到A、B两个码头中的一处,再用货船运送到海岛O,若汽车的行驶速度为50km/h,货船航行的速度为25km/h,问这批物资在哪个码头装船,最早运抵海岛O?(两个码头物资装船所用的时间相同,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)