ћвƒњƒЏ»Ё
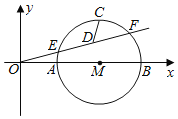
°Њћвƒњ°њ“—÷™ґюіќЇѓ эy£љax2©Б2x£Ђ3Њ≠єэµгA(©Б3£ђ0)£ђP «≈„ќпѕя…ѕµƒ“їЄцґѓµг£Ѓ
£®1£©«уЄ√Їѓ эµƒ±ніп љ£ї
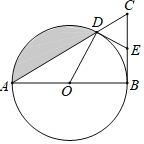
£®2£©»зЌЉЋщ Њ£ђµгP «≈„ќпѕя…ѕ‘ЏµЏґюѕуѕёƒЏµƒ“їЄцґѓµг£ђ«“µгPµƒЇб„ш±кќ™t£ђЅђљ”AC£ђPA£ђPC£Ѓ«у°чACPµƒ√жїэSєЎ”ЏtµƒЇѓ эєЎѕµ љ£ђ≤Ґ«у≥ц°чACPµƒ√жїэ„оіу ±µгPµƒ„ш±к£Ѓ
£®3£©Ѕђљ”BC£ђ‘Џ≈„ќпѕя…ѕ «Јсіж‘ЏµгP£ђ єµ√°ѕPCA£љ°ѕOCB£њ»фіж‘Џ£ђ«у≥цµгPµƒ„ш±к£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ

°Њір∞Є°њ£®1£©y£љ£≠x2£≠2x£Ђ3£ї£®2£©![]() £ђ
£ђ![]() £ї£®3£©
£ї£®3£©![]() їт(£≠4£ђ£≠5)
їт(£≠4£ђ£≠5)
°Њљвќц°њ
£®1£©љЂµгA(-3£ђ0)іш»лљвќц љ«уљвЉіњ…£ї
£®2£©єэµгP„цієѕя£ђ‘т![]() £ђјы”√“—÷™A°ҐCµг„ш±књ…“‘«у≥цAC÷±ѕяµƒљвќц љ£ђі”ґшµ»µљP°ҐQЅљµг„ш±к£ђ‘ўјы”√»эљ«–ќ√жїэєЂ љ«уљвЉіњ…£ї
£ђјы”√“—÷™A°ҐCµг„ш±књ…“‘«у≥цAC÷±ѕяµƒљвќц љ£ђі”ґшµ»µљP°ҐQЅљµг„ш±к£ђ‘ўјы”√»эљ«–ќ√жїэєЂ љ«уљвЉіњ…£ї
£®3£©„ц≥цЄ®÷ъѕя£ђљи÷ъ»эљ«Їѓ эµ√µљ°ѕPCA£љ°ѕOCBµƒєЎѕµ£ђі”ґшµ√µљ±я”л±яµƒєЎѕµ£ђ«уљв≥цќі÷™ э£Ѓ
£®1£©ґюіќЇѓ э![]() єэµгA(-3£ђ0)£ђіъ»л”–0=9a+6+3£ђa=-1£ђ
єэµгA(-3£ђ0)£ђіъ»л”–0=9a+6+3£ђa=-1£ђ
є ќ™іЋЇѓ эљвќц љќ™![]() £ї
£ї
£®2£©єэµгP„чPN![]() AO”ЏµгN£ђљїAC”ЏµгQ£ђ
AO”ЏµгN£ђљїAC”ЏµгQ£ђ
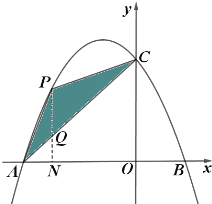
”…£®1£©÷™£ђC(0£ђ3)£ђ…и÷±ѕяACµƒљвќц љќ™y=kx+b£ђ£®k![]() 0£©£ђљЂA(-3£ђ0)°ҐC(0£ђ3)іъ»лy=kx+b£ђµ√
0£©£ђљЂA(-3£ђ0)°ҐC(0£ђ3)іъ»лy=kx+b£ђµ√![]() љвµ√
љвµ√![]() £ђ
£ђ
°а÷±ѕяACµƒљвќц љќ™y=x+3£ђ
°яµгP‘Џ≈„ќпѕя![]() …ѕ£ђµгQ‘Џ÷±ѕяAC…ѕ£ђ
…ѕ£ђµгQ‘Џ÷±ѕяAC…ѕ£ђ
°аP(t£ђ![]() )£ђQ(t£ђt+3)£ђ
)£ђQ(t£ђt+3)£ђ
°аPQ=![]() =
=![]() £ђ
£ђ
![]() £ї
£ї
µ±![]() ±£ђ°чACPµƒ√жїэ„оіу£ђ
±£ђ°чACPµƒ√жїэ„оіу£ђ![]() £ї
£ї
є SєЎ”ЏtµƒЇѓ эєЎѕµ љ![]() £ђP
£ђP![]() £ї
£ї
£®3£©≈„ќпѕя…ѕіж‘ЏµгP£ђ єµ√°ѕPCA£љ°ѕOCB£ђ
єэPµг„чPD![]() AC£ђљїAC”ЏµгD£ђ»зЌЉ
AC£ђљїAC”ЏµгD£ђ»зЌЉ
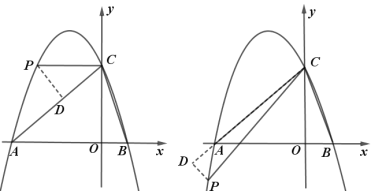
“—÷™≈„ќпѕяЈљ≥ћќ™![]() £ђ
£ђ![]() £ђx=1£ђЉіњ…µ√µљB(1£ђ0)£ђ
£ђx=1£ђЉіњ…µ√µљB(1£ђ0)£ђ
‘т”–OB=1£ђOC=3£ђ![]() £ђ
£ђ
µгP‘Џ≈„ќпѕя…ѕ£ђ…иµгP(a£ђ![]() )£ђ÷±ѕяAC£Їy=x+3£ђ‘т
)£ђ÷±ѕяAC£Їy=x+3£ђ‘т![]() £ђ÷±ѕяPDєэµгP£ђЉіњ…«у≥цPDµƒљвќц љќ™
£ђ÷±ѕяPDєэµгP£ђЉіњ…«у≥цPDµƒљвќц љќ™![]() £ђ”÷“тќ™Dќ™PD”лACµƒљїµг£ђЅ™ЅҐЈљ≥ћ„й”–
£ђ”÷“тќ™Dќ™PD”лACµƒљїµг£ђЅ™ЅҐЈљ≥ћ„й”–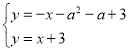 £ђљвµ√”–
£ђљвµ√”–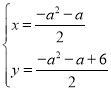 £ђЉіD(
£ђЉіD(![]() £ђ
£ђ
![]() £ђ
£ђ
![]() £ђ
£ђ
°я°ѕPCA£љ°ѕOCB£ђ
°а![]() £ђ
£ђ
°а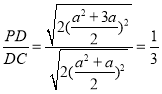 £ђљвµ√a=-4їтa=
£ђљвµ√a=-4їтa=![]() £ђ
£ђ
Ћщ“‘іж‘ЏµгP(-4£ђ-5)їт![]() £Ѓ
£Ѓ

 „яљшќƒ—‘ќƒѕµЅ–ір∞Є
„яљшќƒ—‘ќƒѕµЅ–ір∞Є