Question

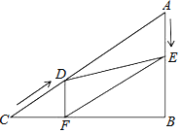
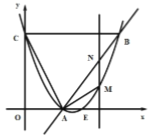
【题目】如图，抛物线与直线经过点，且相交于另一点，抛物线与轴交于点，与轴交于另一点，过点的直线交抛物线于点，且轴，连接，当点在线段上移动时（不与、重合），下列结论正确的是（ ）

A.B.

C.D.四边形的最大面积为13

Answer 1

【答案】C

【解析】

】（1）当MN过对称轴的直线时，解得：BN=，而MN=，BN+MN=5=AB；
（2）由BC∥x轴（B、C两点y坐标相同）推知∠BAE=∠CBA，而△ABC是等腰三角形，∠CBA≠∠BCA，故∠BAC=∠BAE错误；
（3）如上图，过点A作AD⊥BC、BE⊥AC，由△ABC是等腰三角形得到：EB是∠ABC的平分线，∠ACB-∠ANM=∠CAD=∠ABC；
（4）S四边形ACBM=S△ABC+S△ABM，其最大值为．

解：将点A（2，0）代入抛物线y=ax2-x+4与直线y=x+b
解得：a=，b=-，
设：M点横坐标为m，则M（m，m2-m+4）、N（m，m-），
其它点坐标为A（2，0）、B（5，4）、C（0，4），
则AB=BC=5，则∠CAB=∠ACB，
∴△ABC是等腰三角形．
A、当MN过对称轴的直线时，此时点M、N的坐标分别为（，-）、（，），
由勾股定理得：BN=，而MN=，
BN+MN=5=AB，
故本选项错误；
B、∵BC∥x轴（B、C两点y坐标相同），
∴∠BAE=∠CBA，而△ABC是等腰三角形不是等边三角形，
∠CBA≠∠BCA，
∴∠BAC=∠BAE不成立，
故本选项错误；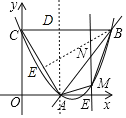

C、如上图，过点A作AD⊥BC、BE⊥AC，
∵△ABC是等腰三角形，
∴EB是∠ABC的平分线，
易证：∠CAD=∠ABE=∠ABC，
而∠ACB-∠ANM=∠CAD=∠ABC，
故本选项正确；
D、S四边形ACBM=S△ABC+S△ABM，
S△ABC=10，
S△ABM=MN（xB-xA）=-m2+7m-10，其最大值为，
故S四边形ACBM的最大值为10+=12.25，故本选项错误．
故选：C．