Question

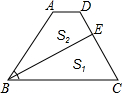如图，在梯形ABCD中，AD∥BC，BE平分∠ABC，且BE⊥CD，CE=2DE，BE把梯形面积分为S₁和S₂两部分，求S₂：S₁．

Answer 1

分析：延长BA、CD交于一点F，从而可判断△BFE≌△BCE，从而由EF=CE=2DE，可得DF=DE=

1

4

FC，易得△FAD∽△FBC，利用面积比等于相似比平方求出S_△FAD，继而得出S₂，这样即可计算S₂：S₁．

解答：
解：延长BA、CD交于一点F，
∵BE平分∠ABC，且BE⊥CD，
∵在△BEF和△BEC中，

∠FBE=∠CBE BE=BE ∠BEF=∠BEC

，
∴△BFE≌△BCE，
∴EF=EC，S_△FBC=2S₁，
又∵CE=2DE，
∴DF=DE=

1

4

FC，
∵AD∥BC，
∴△FAD∽△FBC，
∴

S△FAD

S△FBC

=（

FD

FC

）²=

1

16

，
∴S_△FAD=

1

8

S₁，
∴S₂=S_△FBE-S_△FAD=S₁-

1

8

S₁=

7

8

S₁，
∴S₂：S₁=7：8．

点评：本题考查了相似三角形的判定与性质，解答本题的关键是作出辅助线，同学们注意培养自己的敏感性，一般是角平分线又是高的情况出现，就要寻找等腰三角形．