Question

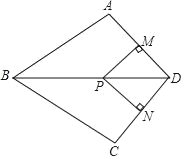
【题目】如图，在正方形ABCD中，E，G分别在边DA，DC上（不与端点重合），且DE=DG，过D点作DF⊥CE，垂足为F．

（1）①∠BCE与∠CDF的大小关系是_______________；

②证明：GF⊥BF；

（2）探究G落在边DC的什么位置时，BF=BC，请说明理由.

Answer 1

【答案】 (1)①∠BCE=∠CDF②见解析;(2) 当G落在线段DC的中点时，BF=BC，理由见解析.

【解析】分析：

（1）①由DF⊥CE可得∠DFC=90°，从而可得∠CDF+∠DCF=90°，结合∠DCF+∠BCE=90°可得∠BCE=∠CDF；

②由已知条件易证△DEF∽△CDF，从而可得,结合①中所得∠BCE=∠CDF可得△DGF∽△BCF，由此可得∠DFG=∠BFC，结合∠DFG+∠GFC =90度可得∠BFC+∠GFC=90°，由此可得∠GFB=90°，从而可得GF⊥BF；

（2）连接BG，若BF=BC，则由（1）中所得∠GFB=90°结合∠BCG=90°，易得△BFG≌△BCG，由此可得GF=GC，在Rt△DFC中，再证GF=GD，即可得到此时点G是CD的中点，由此可知，当点G是CD的中点时，BF=BG.

详解：

（1）①∠BCE=∠CDF

②∵四边形ABCD为正方形

∴CD⊥AD，CB=CD

∵DF⊥CE

∴△DEF∽△CDF

∴

又∵DE=DG，BC=CD

∴

由①知∠BCE=∠CDF

∴△DGF∽△BCF

∴∠DFG=∠BFC

∴∠DFG+∠GFC =∠BFC+∠GFC

即∠GFB=∠DFC=900

∴GF⊥BF

（2）当G落在线段DC的中点时，BF=BC，理由如下：

连接BG，由已知和以上结论知,△BFG和△BCG都是直角三角形,

若BF=BC，又BG=BG

∴Rt△BFG≌Rt△BCG

∴CG=FG

又∵△DFC为直角三角形

∴G为DC的中点.

故当G落在线段DC的中点时，BF=BC.