Question

【题目】阅读理解：若为数轴上三点，若点到的距离是点到的距离的2倍，我们就称点是的优点． 例如图1中：点表示的数为，点表示的数为2． 表示1的点到点的距离是2，到点的距离是1，那么点是的优点；又如，表示0的点到点的距离是1，到点的距离是2，那么点就不是的优点，但点是，的优点．

知识运用：（1）如图2，为数轴上两点，点所表示的数为，点所表示的数为4． 那么数________所表示的点是的优点；（直接填在横线上）

（2）如图3，为数轴上两点，点所表示的数为，点所表示的数为40． 现有一只电子蚂蚁从点出发，以4个单位每秒的速度向左运动，到达点停止． 当为何值时，、和中恰有一个点为其余两点的优点？

Answer 1

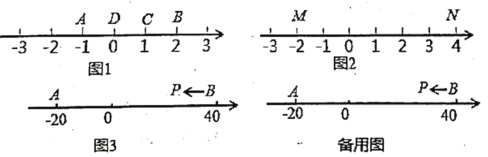
【答案】(1) 2或10；(2) 当t为5秒、10秒或7.5秒时，P、A和B中恰有一个点为其余两点的优点．

【解析】

(1)设所求数为x，根据优点的定义分优点在M、N之间和优点在点N右边，列出方程解方程即可；

(2)根据优点的定义可知分两种情况：①P为(A，B)的优点；②P为(B，A)的优点；③B为(A，P)的优点．设点P表示的数为，根据优点的定义列出方程，进而得出t的值．

(1)设所求数为x，

当优点在M、N之间时，由题意得：，

解得；
当优点在点N右边时，由题意得：，

解得：；
故答案为：2或10；

(2)设点P表示的数为，则，，，
分三种情况：
①P为的优点，
由题意，得，即，
解得：，
∴(秒)；
②P为的优点，
由题意，得，即，
解得：，
∴(秒)；
③B为的优点，
由题意，得，即，
解得：，
此时，点P为AB的中点，即A也为的优点，
∴(秒)；
综上可知，当t为5秒、10秒或7.5秒时，P、A和B中恰有一个点为其余两点的优点．