题目内容
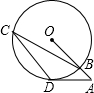如图，AD是⊙O的切线，点D是切点，OA与⊙O交于点B，CD∥OA交⊙O于点C，连接CB．若∠A=50°，则∠OBC等于
- A.40°
- B.30°
- C.25°
- D.20°
D
分析：连接OD，在直角三角形OAD中，求得∠O，再根据圆周角定理得出∠C，由平行线的性质求出∠OBC．
解答：
解：连接OD，
∴∠ODA=90°，
∵∠A=50°，∴∠O=40°，
∴∠C=20°，
∵CD∥OA，∴∠C=∠OBC，
∴∠OBC=20°，
故选D．
点评：本题考查了切线的性质、平行线的性质、以及圆周角定理，是基础知识要熟练掌握．
分析：连接OD，在直角三角形OAD中，求得∠O，再根据圆周角定理得出∠C，由平行线的性质求出∠OBC．
解答：
解：连接OD，∴∠ODA=90°，
∵∠A=50°，∴∠O=40°，
∴∠C=20°，
∵CD∥OA，∴∠C=∠OBC，
∴∠OBC=20°，
故选D．
点评：本题考查了切线的性质、平行线的性质、以及圆周角定理，是基础知识要熟练掌握．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
如图，AD是圆O的直径，BC切圆O于点D，AB，AC与圆O相交于点E，F．求证：AE•AB=AF•AC．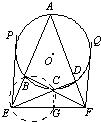
7、如图，ABCD是⊙O的内接四边形，延长AB和DC相交于E，延长AB和DC相交于E，延长AD和BC相交于F，EP和FQ分别切⊙O于P、Q．求证：EP2+FQ2=EF2．
18、如图，AB是⊙O的直径，直线EF切⊙O于点B，点C和点D是⊙O上的两点，若∠CBE=40°，AD=CD，则∠BCD=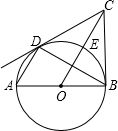
如图，AB是⊙O的直径，BC切⊙O于B，弦AD∥OC，OC交⊙O于E．
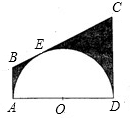已知：如图，AD是半圆O的直径，AB、CD与半圆O切于点A、D，E为半圆O上一点，过点E的直线交AB于点B，交CD交点C，且CD=CE．