Question

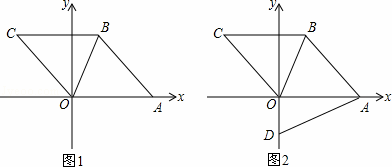
平面直角坐标系中，四边形ABCD是菱形，点C的坐标为（﹣3，4），点A在x轴的正半轴上，O为坐标原点，连接OB，抛物线y=ax²+bx+c经过C、O、A三点．

（1）直接写出这条抛物线的解析式；

（2）如图1，对于所求抛物线对称轴上的一点E，设△EBO的面积为S₁，菱形ABCD的面积为S₂，当S₁≤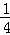S₂时，求点E的纵坐标n的取值范围；

（3）如图2，D（0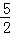，﹣）为y轴上一点，连接AD，动点P从点O出发，以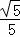个单位/秒的速度沿OB方向运动，1秒后，动点Q从O出发，以2个单位/秒的速度沿折线O﹣A﹣B方向运动，设点P运动时间为t秒（0＜t＜6），是否存在实数t，使得以P、Q、B为顶点的三角形与△ADO相似？若存在，求出相应的t值；若不存在，请说明理由．

Answer 1

       解：（1）根据题意得：，

解得：，

则抛物线的解析式是：y=x²﹣x；

（2）设BC与y轴相交于点G，则S₂=OG•BC=20，

∴S₁≤5，

又OB所在直线的解析式是y=2x，OB==2，

∴当S₁=5时，△EBO的OB边上的高是．

如图1，设平行于OB的直线为y=2x+b，则它与y轴的交点为M（0，b），与抛物线对称轴x=交于点E（，n）．

过点O作ON⊥ME，点N为垂足，若ON=，由△MNO∽△OGB，得OM=5，

∴y=2x﹣5，

由，

解得：y=0，

即E的坐标是（，0）．

∵与OB平行且到OB的距离是的直线有两条．

∴由对称性可得另一条直线的解析式是：y=2x+5．

则E′的坐标是（，10）．

由题意得得，n的取值范围是：0≤n≤10且n≠5．

（3）如图2，动点P、Q按题意运动时，

当1＜t＜3.5时，

OP=t，BP=2﹣t，OQ=2（t﹣1），

连接QP，当QP⊥OP时，有=，

∴PQ=（t﹣1），

若=，则有=，

又∵∠QPB=∠DOA=90°，

∴△BPQ∽△AOD，

此时，PB=2PQ，即2﹣t=（t﹣1），

10﹣t=8（t﹣1），

∴t=2；

当3.5≤t≤6时，QB=10﹣2（t﹣1）=12﹣2t，连接QP．

若QP⊥BP，

则有∠PBQ=∠ODA，

又∵∠QPB=∠AOD=90°，

∴△BPQ∽△DOA，

此时，PB=PB，即12﹣2t=（2﹣t），12﹣2t=10﹣t，

∴t=2（不合题意，舍去）．

若QP⊥BQ，则△BPQ∽△DAO，

此时，PB=BQ，

即2﹣t=（12﹣2t），2﹣t=12﹣2t，

解得：t=．

则t的值为2或．