题目内容
 学校会议室采用大小相同的长方形木块镶嵌地面,第一次铺2块,如图1,第二次把第一次铺的部分完全围起来,如图2,第三次把第二次铺的部分完全围起来,如图3…依此类推.如果把从开始到第n次铺完后总共用的木块数记作an,把第n次镶嵌时用来围铺前一次木块所用的木块(即周围一圈的木块)数记作bn.则:
学校会议室采用大小相同的长方形木块镶嵌地面,第一次铺2块,如图1,第二次把第一次铺的部分完全围起来,如图2,第三次把第二次铺的部分完全围起来,如图3…依此类推.如果把从开始到第n次铺完后总共用的木块数记作an,把第n次镶嵌时用来围铺前一次木块所用的木块(即周围一圈的木块)数记作bn.则:
(1)a3=______;b3=______;
(2)bn=______(用含n的代数式表示)
(3)a99+b100=______.
解:(1)根据图形可得:a3=30;b3=18;
(2)观察前边的三个图形,发现,
第一次镶嵌所使用的木块数为2,
第二次镶嵌所使用的木块数为10,
第三次镶嵌所使用的木块数为18,
则第n次镶嵌所使用的木块数为2n(2n-1)-(2n-2)(2n-3)=8n-6.
(3)第一次铺了:1×2=2(块),
第二次铺了:3×4=12(块),
第三次铺了:5×6=30(块),
…
第n次铺了(2n-1)×2n块,
∴a99+b100=118×117+8×100-6=13806+800-6=14600
故答案为:(1)30;18 (2)8n-6 (3)14600
分析:(1)根据图形数出来即可得到答案;
(2)结合图形发现:第一次镶嵌所使用的木块数为1×2=2,第二次镶嵌所使用的木块数为3×4-1×2=10,第三次镶嵌所使用的木块数为5×6-3×4=18,从数据上,推而广之即可;
(3)根据题意,第一次铺了1×2=2(块),第二次铺了3×4=12(块),第三次铺了5×6=30(块),依次推下去,第四次铺了7×8=56(块),…第n次铺了(2n-1)×2n块,代入数据即可求解.
点评:考查了规律型:图形的变化,此题要哪个结合图形和数字之间的规律进行推广.
(2)观察前边的三个图形,发现,
第一次镶嵌所使用的木块数为2,
第二次镶嵌所使用的木块数为10,
第三次镶嵌所使用的木块数为18,
则第n次镶嵌所使用的木块数为2n(2n-1)-(2n-2)(2n-3)=8n-6.
(3)第一次铺了:1×2=2(块),
第二次铺了:3×4=12(块),
第三次铺了:5×6=30(块),
…
第n次铺了(2n-1)×2n块,
∴a99+b100=118×117+8×100-6=13806+800-6=14600
故答案为:(1)30;18 (2)8n-6 (3)14600
分析:(1)根据图形数出来即可得到答案;
(2)结合图形发现:第一次镶嵌所使用的木块数为1×2=2,第二次镶嵌所使用的木块数为3×4-1×2=10,第三次镶嵌所使用的木块数为5×6-3×4=18,从数据上,推而广之即可;
(3)根据题意,第一次铺了1×2=2(块),第二次铺了3×4=12(块),第三次铺了5×6=30(块),依次推下去,第四次铺了7×8=56(块),…第n次铺了(2n-1)×2n块,代入数据即可求解.
点评:考查了规律型:图形的变化,此题要哪个结合图形和数字之间的规律进行推广.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 寒假假期,某学校准备组织部分学生到A、B、C三地参观学习.学校购买前往各地的车票种类和数量绘制成统计图,如图.根据统计图回答下列问题:
寒假假期,某学校准备组织部分学生到A、B、C三地参观学习.学校购买前往各地的车票种类和数量绘制成统计图,如图.根据统计图回答下列问题:
 学校会议室采用大小相同的长方形木块镶嵌地面,第一次铺2块,如图1,第二次把第一次铺的部分完全围起来,如图2,第三次把第二次铺的部分完全围起来,如图3…依此类推.如果把从开始到第n次铺完后总共用的木块数记作an,把第n次镶嵌时用来围铺前一次木块所用的木块(即周围一圈的木块)数记作bn.则:
学校会议室采用大小相同的长方形木块镶嵌地面,第一次铺2块,如图1,第二次把第一次铺的部分完全围起来,如图2,第三次把第二次铺的部分完全围起来,如图3…依此类推.如果把从开始到第n次铺完后总共用的木块数记作an,把第n次镶嵌时用来围铺前一次木块所用的木块(即周围一圈的木块)数记作bn.则: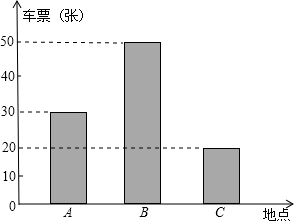 寒假假期,某学校准备组织部分学生到A、B、C三地参观学习.学校购买前往各地的车票种类和数量绘制成统计图,如图.根据统计图回答下列问题:
寒假假期,某学校准备组织部分学生到A、B、C三地参观学习.学校购买前往各地的车票种类和数量绘制成统计图,如图.根据统计图回答下列问题: