题目内容
设a，b为正数，则有如下结论：①a+b=2，则
≤1；②a+b=5，则
≤
；③a+b=6，则
≤3；
根据以上所提供的规律猜想：
（1）若a+b=20，则
≤
（2）对任何正数x，y总有
≤
．
| ab |
| ab |
| 5 |
| 2 |
| ab |
根据以上所提供的规律猜想：
（1）若a+b=20，则
| ab |
10
10
； （2）对任何正数x，y总有
| xy |
| x+y |
| 2 |
| x+y |
| 2 |
分析：（1）根据题中的规律变形后，将a+b代入即可求出值；
（2）归纳总结得到结果即可．
（2）归纳总结得到结果即可．
解答：解：（1）∵a+b=20，
∴根据提供的规律得：
≤
=10；
（2）根据提供的规律得：
≤
．
故答案为：（1）10；（2）
∴根据提供的规律得：
| ab |
| a+b |
| 2 |
（2）根据提供的规律得：
| xy |
| x+y |
| 2 |
故答案为：（1）10；（2）
| x+y |
| 2 |
点评：此题考查了完全平方公式的运用，属于规律型试题，弄清题中的规律是解本题的关键．
练习册系列答案
相关题目
设ab≠0，且函数f1（x）=x2+2ax+4b与f2（x）=x2+4ax+2b有相同的最小值u；函数f3（x）=-x2+2bx+4a与f4（x）=-x2+4bx+2a有相同的最大值v；则u+v的值（ ）
| A、必为正数 | B、必为负数 | C、必为0 | D、符号不能确定 |
与
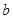的大小，可先求出
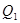元，乙两次购买粮食的平均单价为
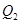元，
；②
；③
；
______； 
______．