题目内容
设ab≠0,且函数f1(x)=x2+2ax+4b与f2(x)=x2+4ax+2b有相同的最小值u;函数f3(x)=-x2+2bx+4a与f4(x)=-x2+4bx+2a有相同的最大值v;则u+v的值( )
| A、必为正数 | B、必为负数 | C、必为0 | D、符号不能确定 |
分析:本题给出四个函数的解析式及两条重要信息f1(x)与f2(x)有相同的最小值u;f3(x)与f4(x)有相同的最大值v,将函数化为顶点式,再根据条件列出等式即可求解此题.
解答:解:∵f1(x)=x2+2ax+4b=(x+a)2+4b-a2≥4b-a2,
f2(x)=x2+4ax+2b=(x+2a)2+2b-4a2≥2b-4a2,
已知4b-a2=u=2b-4a2,得-2b=3a2①
∵ab≠0,
∴b<0,
又∵f3(x)=-(x-b)2+4a+b2≤4a+b2,
f4(x)=-(x-2b)2+2a+4b2≤2a+4b2;
已知4a+b2=v=2a+4b2,得2a=3b2,②
∵ab≠0,
∴a>0,
∴3a-3b+2>0,
∴②-①得,2(a+b)=3(b2-a2),
解得a+b=0或b-a=
(舍去),
当a+b=0时,2(u+v)=(6b-5a2)+(6a+5b2)=(a+b)[6+5(b-a)]=0,
∴u+v=0,
故选C.
f2(x)=x2+4ax+2b=(x+2a)2+2b-4a2≥2b-4a2,
已知4b-a2=u=2b-4a2,得-2b=3a2①
∵ab≠0,
∴b<0,
又∵f3(x)=-(x-b)2+4a+b2≤4a+b2,
f4(x)=-(x-2b)2+2a+4b2≤2a+4b2;
已知4a+b2=v=2a+4b2,得2a=3b2,②
∵ab≠0,
∴a>0,
∴3a-3b+2>0,
∴②-①得,2(a+b)=3(b2-a2),
解得a+b=0或b-a=
| 2 |
| 3 |
当a+b=0时,2(u+v)=(6b-5a2)+(6a+5b2)=(a+b)[6+5(b-a)]=0,
∴u+v=0,
故选C.
点评:本题考查了二次函数的最值,难度较大,做题时关键是将函数的标准形式化为顶点形式.

练习册系列答案
相关题目
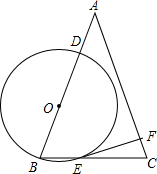 、BC相交于D、E两点,但⊙O与边AC不相交,又EF⊥AC,垂足为F.设OB=x,CF=y.
、BC相交于D、E两点,但⊙O与边AC不相交,又EF⊥AC,垂足为F.设OB=x,CF=y.