题目内容
如图，点A、B在反比例函数y=
（k＞0，x＞0）的图象上，过点A、B作x轴的垂线，垂足分别为M、N，延长线段AB交x轴于点C，若OM=MN=NC，△AOC的面积为6，则k的值为________．
4
分析：设OM的长度为a，利用反比例函数解析式表示出AM的长度，再求出OC的长度，然后利用三角形的面积公式列式计算恰好只剩下k，然后计算即可得解．
解答：设OM=a，
∵点A在反比例函数y=，
∴AM=
，
∵OM=MN=NC，
∴OC=3a，
∴S△AOC=
•OC•AM=×3a×=
k=6，
解得k=4．
故答案为：4．
点评：本题综合考查了反比例函数与三角形的面积，根据反比例函数的特点，用OM的长度表示出AM、OC的长度，相乘恰好只剩下k是解题的关键，本题设计巧妙，是不错的好题．
分析：设OM的长度为a，利用反比例函数解析式表示出AM的长度，再求出OC的长度，然后利用三角形的面积公式列式计算恰好只剩下k，然后计算即可得解．
解答：设OM=a，
∵点A在反比例函数y=
，∴AM=
，∵OM=MN=NC，
∴OC=3a，
∴S△AOC=
•OC•AM=×3a×=k=6，解得k=4．
故答案为：4．
点评：本题综合考查了反比例函数与三角形的面积，根据反比例函数的特点，用OM的长度表示出AM、OC的长度，相乘恰好只剩下k是解题的关键，本题设计巧妙，是不错的好题．
练习册系列答案
相关题目
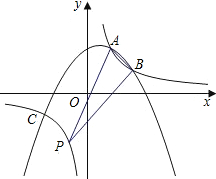如图，抛物线y=ax2+bx+c经过点A（1，2）、B（2，1）和C（-2，-1）三点．
如图，△P1OA1，△P2A1A2，△P3A2A3，…，是等腰直角三角形，点P1，P2，P3，…，在反比列函数y=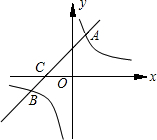
次函数y=mx+b的图象与x轴交于点C．
如图，△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形，点P1、P2、P3、…、P100在反比列函数