题目内容
15.圆内接正三角形的边长是12cm,则该圆的半径长是 ( )| A. | 3$\sqrt{3}$cm | B. | 4$\sqrt{3}$cm | C. | 3$\sqrt{2}$cm | D. | 4$\sqrt{2}$cm |
分析 利用正三角形的性质找到由内切圆半径,外接圆半径和边长的一半所组成的三角形(如△OBD),然后进行计算可求出外接圆半径.
解答 解:如图,△ABC是⊙O的边长为2的内接正三角形.
连OB,OA,
∵△ABC是正三角形,
∴AO垂直平分BC,设垂足为D.
∴BD=CD=6;
又∵∠OBD=30°,
∴OD=2$\sqrt{2}$,则OB=2OD=4$\sqrt{2}$
故选D.
点评 本题考查正多边形与圆,正三角形的性质、解直角三角形等知识,解题的关键是学会填空常用辅助线,构造直角三角形解决问题.

练习册系列答案
相关题目
6.若一元二次方程的两根分别是-2和5,则这个方程可能为( )
| A. | x2-10x+3=0 | B. | x2-3x-10=0 | C. | x2+3x-10=0 | D. | x2-3x+10=0 |
6. 如图,在△ABC中,∠ACB=90°,∠B=32°.分别以A、B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于点D和E,连接DE,交AB于点F,连接CF,则∠AFC的度数为( )
如图,在△ABC中,∠ACB=90°,∠B=32°.分别以A、B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于点D和E,连接DE,交AB于点F,连接CF,则∠AFC的度数为( )
 如图,在△ABC中,∠ACB=90°,∠B=32°.分别以A、B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于点D和E,连接DE,交AB于点F,连接CF,则∠AFC的度数为( )
如图,在△ABC中,∠ACB=90°,∠B=32°.分别以A、B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于点D和E,连接DE,交AB于点F,连接CF,则∠AFC的度数为( )| A. | 60° | B. | 62° | C. | 64° | D. | 65° |
20. 如图,正五边形ABCDE内接于⊙O,则∠OAB的度数为( )
如图,正五边形ABCDE内接于⊙O,则∠OAB的度数为( )
 如图,正五边形ABCDE内接于⊙O,则∠OAB的度数为( )
如图,正五边形ABCDE内接于⊙O,则∠OAB的度数为( )| A. | 36° | B. | 72° | C. | 54° | D. | 108° |
7. 如图,过点A作BC的垂线段,垂足坐标是( )
如图,过点A作BC的垂线段,垂足坐标是( )
 如图,过点A作BC的垂线段,垂足坐标是( )
如图,过点A作BC的垂线段,垂足坐标是( )| A. | (2,-2) | B. | (-5,-2) | C. | (-2.5,2) | D. | (2,4) |

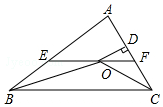 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论.
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论.