Question

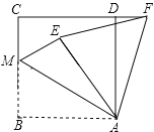
【题目】如图，在正方形ABCD中，AB=4，M是BC中点，连接AM，将△ABM沿AM折叠得到△AEM，将△ABM绕点A顺时针旋转90°得到△ADF，连接EF，则EF的长为（　　）

A.2B.C.4D.2

Answer 1

【答案】D

【解析】

由旋转的性质，折叠的性质可得BE⊥AM，BE=2BP，BM=DF=2，AB=AE=4，由三角形面积公式可求BP=，由勾股定理可求AG的长，可得HF，HE的长，由勾股定理可求EF的长．

如图，连接BE，交AM于点P，过点E作EH⊥CD，延长HE交AB于点G，

∵在正方形ABCD中，AB=4，M是BC中点，

∴BM=2，

∴AM==2

∵将△ABM沿AM折叠得到△AEM，将△ABM绕点A顺时针旋转90°得到△ADF，

∴BE⊥AM，BE=2BP，BM=DF=2，AB=AE=4，

∵S△ABM=×AB×BM=×AM×BP

∴2×4=2×BP

∴BP=

∴BE=2BP=

∵AB∥CD，EH⊥CD

∴HG⊥AB，且EH⊥CD，∠DAB=90°

∴AD=GH=4，AG=HD，

∵EG2=BE2-BG2=AE2-AG2，

∴-（4-AG）2=16-AG2，

∴AG=，

∴EG=，HD=

∴HE=，HF=

∴EF==2

故选：D．