题目内容
19.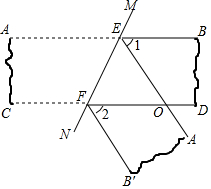 如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.
如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.(1)试说明∠1=∠2;
(2)已知∠2=40°,求∠BEF的度数.
分析 (1)根据平行线的性质得到∠MEB=∠NFD,∠NEA′=∠MFB′,根据角的和差即可得到结论;
(2)由折叠知,∠B′FN=$\frac{180°-∠2}{2}$=70°,根据平行线的性质得到∠A′EN=∠B′FN=70°,即可得到结论.
解答 解:(1)∵AB∥CD,∴∠MEB=∠MFD,
∵A′E∥B′F,
∴∠MEA′=∠MFB′,
∴∠MEA′-∠MEB=∠MFB′-∠MFD,
即∠1=∠2;
(2)由折叠知,∠B′FN=$\frac{180°-∠2}{2}$=70°,
∵A′E∥B′F,
∴∠A′EN=∠B′FN=70°,
∵∠1=∠2,
∴∠BEF=70°+40°=110°.
点评 本题考查了平行线的性质,折叠的性质,熟练掌握平行线的性质是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
7.为增强公民的节约意识,合理利用水资源,某市采用价格调控手段达到节水的目的,该市自来水的收费价格见价目表
(1)若甲用户3月份的用水16m3,则应收水费64元.
(2)若乙用户2、3月份共用水18m3(3月份用水量低于2月份用水量),共缴费50元,乙用户2、3月份的用水量各是多少?
| 每月用水量 | 单价(元/m3) |
| 不超过8m3的部分 | 2 |
| 超出8m3,但不超出12m3的部分 | 4 |
| 超出12m3的部分 | 8 |
(2)若乙用户2、3月份共用水18m3(3月份用水量低于2月份用水量),共缴费50元,乙用户2、3月份的用水量各是多少?
 已知平面直角坐标系中,一次函数y=-2x+4的图象与x轴相交于点A,与y轴相交于点B,求A、B两点的坐标,并在图中画出该一次函数的图象.
已知平面直角坐标系中,一次函数y=-2x+4的图象与x轴相交于点A,与y轴相交于点B,求A、B两点的坐标,并在图中画出该一次函数的图象. 按下列要求画图并填空:
按下列要求画图并填空: