题目内容
 如图所示,△COB是由△AOB经过某种变换后得到的图形,观察点A与点C的坐标之间的关系,解答下列问题:
如图所示,△COB是由△AOB经过某种变换后得到的图形,观察点A与点C的坐标之间的关系,解答下列问题:(1)若点M的坐标为(x、y),则它的对应点N的坐标为
(2)若点P(a,2)与点Q(-3,b)关于x轴对称,求代数式
| 1 |
| ab |
| 1 |
| (a-1)(b-1) |
| 1 |
| (a-2)(b-2) |
| 1 |
| (a-10)(b-10) |
分析:(1)根据关于坐标轴对称的点的特点确定点的坐标即可;
(2)利用两点关于x轴对称,分别求得a、b的值,代入代数式求值即可.
(2)利用两点关于x轴对称,分别求得a、b的值,代入代数式求值即可.
解答:解:(1)由图象知点M和点N关于x轴对称,
∵点M的坐标为(x、y),
∴点N的坐标为(x,-y);
(2)∵点P(a,2)与点Q(-3,b)关于x轴对称,
∴a=-3,b=-2,
∴
+
+
+…+
=
+
+
+…+
,
=
-
+
-
+…+
-
,
=
-
,
=
.
∵点M的坐标为(x、y),
∴点N的坐标为(x,-y);
(2)∵点P(a,2)与点Q(-3,b)关于x轴对称,
∴a=-3,b=-2,
∴
| 1 |
| ab |
| 1 |
| (a-1)(b-1) |
| 1 |
| (a-2)(b-2) |
| 1 |
| (a-10)(b-10) |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 20 |
| 1 |
| 156 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 13 |
=
| 1 |
| 2 |
| 1 |
| 13 |
=
| 11 |
| 26 |
点评:本题考查了坐标的图形变化及分式的化简求值,此类题目相对较易,只需牢记对称点的坐标的变化方法即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,0是直线上一点,∠COB=α,OD平分∠AOC,OE平分∠COB.试说明∠DOC和∠COE互余.
如图所示,0是直线上一点,∠COB=α,OD平分∠AOC,OE平分∠COB.试说明∠DOC和∠COE互余. 如图所示,AOB是一条直线,∠AOD:∠DOB=3:1,OD平分∠COB.
如图所示,AOB是一条直线,∠AOD:∠DOB=3:1,OD平分∠COB.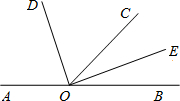 如图所示,O是直线AB上一点,∠COB=46°,OD平分∠AOC,OE平分∠COB,则∠DOE=
如图所示,O是直线AB上一点,∠COB=46°,OD平分∠AOC,OE平分∠COB,则∠DOE= 如图所示,△COB是由△AOB经过某种变换后得到的图形,观察点A与点C的坐标之间的关系,解答下列问题:
如图所示,△COB是由△AOB经过某种变换后得到的图形,观察点A与点C的坐标之间的关系,解答下列问题: …
… 的值.
的值.