Question

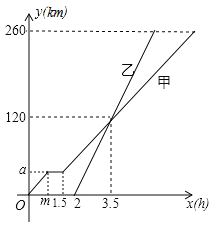
【题目】甲、乙两车都从A地驶向B地，并以各自的速度匀速行驶甲车比乙车早行驶，甲车途中休息了设甲车行驶时间为，下图是甲乙两车行驶的距离与的函数图象，根据题中信息回答问题：

填空：______，______；

当乙车出发后，求乙车行驶路程与的函数解析式，并写出相应的x的取值范围；

当甲车行驶多长时间时，两车恰好相距50km？请直接写出答案．

Answer 1

【答案】（1）1，40；（2）y=80x-160, （3），，，．

【解析】

用休息后出发时间减去即为m的值；根据甲匀速行驶即可求出a的值；

设乙行驶路程，找出图象上和代入即可求出k，b值，从而求出解析式；

用待定系数法求出甲路程y与时间x的关系，由“两车相距50km”得到列出方程求出x即为答案．

．

甲车匀速行驶，

．

设乙行驶路程，依题意得，

，

解得，．

乙行驶路程．

当时，，解得，．

自变量取值范围为．

设甲在后一段路程，依题意得，

，解得．

甲路程．

当时，由两车相距50km得，

解得，．

当时，若两车相距50km，则

解得，．

当时，乙车已到达目的地，两车相距50km，则

解得，．

故答案为，，，．