Question

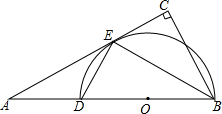如图，在Rt△ABC中，∠C=90°，点D在AB上，以BD为直径的圆O与AC交于点E，且BC平分∠ABC，
（1）判断直线AC与圆⊙O的位置关系，并说明理由；
（2）若AD=2，AE=2

3

，求圆⊙O的面积．

Answer 1

考点：切线的判定,勾股定理

专题：

分析：（1）连接OE．欲证AC是⊙O的切线，只需证明AC⊥OE即可；
（2）由根据勾股定理得出圆的半径长，由此得解．

解答：解：（1）直线AC与圆⊙O相切，
理由：连接EO，
∵OB=OE，
∴∠OBE=∠OEB，
∵∠OBE=∠CBE，
∴∠OEB=∠CBE，
∴OE∥BC，
∴∠AEO=∠C=90°，
∴直线AC是圆⊙O的切线；

（2）设半径为r，根据勾股定理得：
（2

3

）²+r²=（r+2）²，
解得：r=2，
则圆⊙O的面积为：4π．

点评：本题考查了切线的判定定理（经过半径的外端且垂直于这条半径的直线是圆的切线）和勾股定理的运用，具有一定的综合性．