题目内容
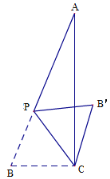
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.

(1)点![]() 的坐标为___________;
的坐标为___________;
(2)连结![]() ,求
,求![]() 的正切值;
的正切值;
(3)抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() (
(![]() 、
、![]() 不重合),使
不重合),使![]() 与
与![]() 全等?若存在,求出点
全等?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]()
【解析】
(1)根据题意即可求出点C的坐标,然后根据关于y轴对称的两点坐标关系即可求出结论;
(2)过点![]() 作
作![]() 于
于![]() ,先求出OB和CD,再利用勾股定理求出BC和BD,然后根据三角形面积的两种求法即可求出DM,再利用勾股定理求出BM,即可求出结论.
,先求出OB和CD,再利用勾股定理求出BC和BD,然后根据三角形面积的两种求法即可求出DM,再利用勾股定理求出BM,即可求出结论.
(3)根据对称轴公式即可求出二次函数的解析式,然后根据全等三角形的对应情况分类讨论,分别画出对应的图形,然后根据全等三角形的性质、锐角三角函数、平行四边形的判定及性质即可求出结论.
解:(1)∵点![]() ,点
,点![]() 为
为![]() 中点,
中点,
∴点C的坐标为(-1,0)
∵点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.
∴点D的坐标为![]() .
.
故答案为:![]() .
.
(2)如图,过点![]() 作
作![]() 于
于![]() ,
,
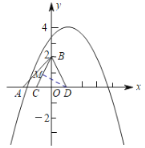
由题易得,![]() ,
,![]() ,
,![]() ,
,
又![]() ,则
,则![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
∴![]() .
.
(3)由题可得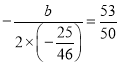 ,
,
解得![]() ,
,
则抛物线所对应的函数解析式为![]() ,
,
①如图,当![]() 时,因为点
时,因为点![]() 不与点
不与点![]() 重合,则点
重合,则点![]() 只能在
只能在![]() 的右侧,过点
的右侧,过点![]() 作
作![]() 轴于
轴于![]() ,
,
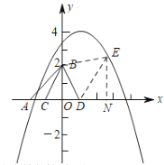
由全等的性质可知,![]() ,
,
∵![]() ,且
,且![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() .
.
又![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,此时点
,此时点![]() 在抛物线上,且符合题意;
在抛物线上,且符合题意;
②如图,当![]() ,且点
,且点![]() 在
在![]() 的右侧时,
的右侧时,
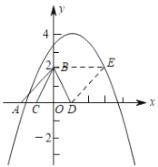
易得四边形![]() 是平行四边形,则
是平行四边形,则![]() ,
,
此时点![]() 在抛物线上,且符合题意;
在抛物线上,且符合题意;
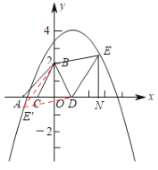
③如图,当![]() ,且点
,且点![]() 在
在![]() 的左侧时,记此时的点
的左侧时,记此时的点![]() 为
为![]() ,
,
则![]() 与①中的
与①中的![]() 组成平行四边形
组成平行四边形![]() ,
,
易得![]() ,此时点
,此时点![]() 在抛物线上,且符合题意;
在抛物线上,且符合题意;
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目