题目内容
如图,在![]() 中,
中,![]() ,以AC为直径作
,以AC为直径作![]() ,交AB于D,过O作OE//AB,交BC于E,求证:ED为
,交AB于D,过O作OE//AB,交BC于E,求证:ED为![]() 的切线.
的切线.

连OD,

∵OE//AB
∴∠EOC=∠A,∠EOD=∠ODA
又∵OA=OD
∴∠A=∠ODA
∴∠EOC=∠EOD
又OE=OE OC=OD
∴△EOC≌△EOD
∴∠EDO=∠ECO 又∠C=90°
∴∠EDO=90°
即ED⊥DO 而点D在 上 ∴ED为
上 ∴ED为![]() 的切线
的切线
解析:连接OD,CD,求出∠BDC=90°,根据OE∥AB和OA=OC求出BE=CE,推出DE=CE,根据SSS证△ECO≌△EDO,推出∠EDO=∠ACB=90°即可

练习册系列答案
相关题目
 中,
中, ,以AC为直径作
,以AC为直径作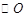 ,交AB于D,过O作OE//AB,交BC于E,求证:ED为
,交AB于D,过O作OE//AB,交BC于E,求证:ED为
 中,
中, ,以AC为直径作
,以AC为直径作 ,交AB于D,过O作OE//AB,交BC于E,求证:ED为
,交AB于D,过O作OE//AB,交BC于E,求证:ED为
 中,
中, ,以AC为直径作⊙O交AB于点D.
,以AC为直径作⊙O交AB于点D. ,求线段BD的长.
,求线段BD的长.