题目内容
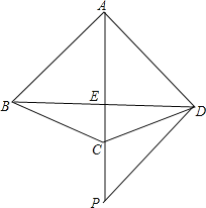
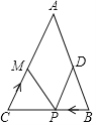
【题目】如图，
，
，点D为
的中点，点P在边
上以每秒
的速度由点B向点C运动，同时，点M在边
上由点C向点A匀速运动．
（1）当点M的运动速度与点P的运动速度相同，经过1秒后，
与
是否全等？请说明理由；
（2）若点M的运动速度与点P的运动速度不相等，当点M的运动速度为多少时，能够使与全等？
【答案】（1）
与
全等，理由见解析；（2）
．
【解析】
（1）△BPD与△CMP全等，根据SAS即可判断；
（2）由
，利用全等三角形的性质可知CM=BD=8，PC=PB=5，推出t=
，从而可得出点M的运动速度．
解：（1）结论：与全等．
理由：
时，
，
，
，
，
，
，
在
和
中，
，
≌
(SAS)；
（2）由题意与全等，
，
，
，
，
点M的运动速度
．
答：当点M的运动速度为
时，能够使与全等．
练习册系列答案
相关题目
