题目内容
双曲线y= (x>0)与直线y=x在坐标系中的图象如图所示,点A、B在直线上AC、BD分别平行y轴,交曲线于C、D两点,若BD=2AC 则4OC2-OD2的值为 .
(x>0)与直线y=x在坐标系中的图象如图所示,点A、B在直线上AC、BD分别平行y轴,交曲线于C、D两点,若BD=2AC 则4OC2-OD2的值为 .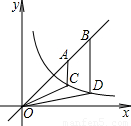
【答案】分析:根据A,B两点在直线y=x上,分别设A,B两点的坐标为(a,a),(b,b),得到点C的坐标为(a,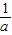 ),点D的坐标为(b,
),点D的坐标为(b, ),线段AC=a-
),线段AC=a-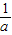 ,线段BD=b-
,线段BD=b-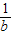 ,根据BD=2AC,有b-
,根据BD=2AC,有b- =2(a-
=2(a-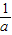 ),然后利用勾股定理进行计算求出4OC2-OD2的值.
),然后利用勾股定理进行计算求出4OC2-OD2的值.
解答:解:设A(a,a),B(b,b),则C(a,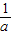 ),D(b,
),D(b,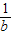 ),
),
AC=a-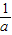 ,BD=b-
,BD=b-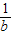 ,
,
∵BD=2AC,
∴b- =2(a-
=2(a-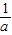 ),
),
4OC2-OD2
=4(a2+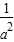 )-(b2+
)-(b2+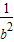 )
)
=4[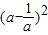 +2]-[
+2]-[ +2]
+2]
=4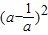 +8-4
+8-4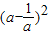 -2
-2
=6.
故答案为:6.
点评:本题考查的是反比例函数综合题,根据直线与反比例函数的解析式,设出点A,B的坐标后可以得到点C,D的坐标,运用勾股定理进行计算求出代数式的值.
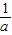 ),点D的坐标为(b,
),点D的坐标为(b, ),线段AC=a-
),线段AC=a-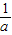 ,线段BD=b-
,线段BD=b-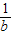 ,根据BD=2AC,有b-
,根据BD=2AC,有b- =2(a-
=2(a-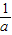 ),然后利用勾股定理进行计算求出4OC2-OD2的值.
),然后利用勾股定理进行计算求出4OC2-OD2的值.解答:解:设A(a,a),B(b,b),则C(a,
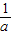 ),D(b,
),D(b,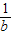 ),
),AC=a-
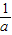 ,BD=b-
,BD=b-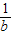 ,
,∵BD=2AC,
∴b-
 =2(a-
=2(a-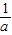 ),
),4OC2-OD2
=4(a2+
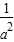 )-(b2+
)-(b2+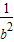 )
)=4[
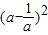 +2]-[
+2]-[ +2]
+2]=4
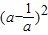 +8-4
+8-4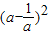 -2
-2=6.
故答案为:6.
点评:本题考查的是反比例函数综合题,根据直线与反比例函数的解析式,设出点A,B的坐标后可以得到点C,D的坐标,运用勾股定理进行计算求出代数式的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
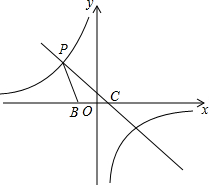 如图,点C(1,0)是x轴上一点,直线PC与双曲线
如图,点C(1,0)是x轴上一点,直线PC与双曲线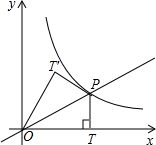 (2011•泉州质检)如图,点P(m,1)是双曲线y=
(2011•泉州质检)如图,点P(m,1)是双曲线y=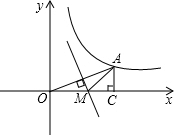 (2012•漳州)如图,点A(3,n)在双曲线y=
(2012•漳州)如图,点A(3,n)在双曲线y=