题目内容
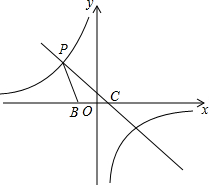 如图,点C(1,0)是x轴上一点,直线PC与双曲线y=
如图,点C(1,0)是x轴上一点,直线PC与双曲线y=| k | x |
(1)求双曲线和直线PC的解析式.
(2)设P′点是直线PC上一点,且点P′与点P关于点C对称,直接写出点P′的坐标.
分析:(1)过P作PE⊥x轴于E,设BE=a,求出CE=
a,根据垂直平分线性质和三角形的外角性质求出∠EPB=30°,推出PE=
BE,得出方程a+4=
×
a,求出a,即可得出P的坐标,
代入y=
即可求出反比例函数的表达式,设直线PC的解析式是y=mx+b把P、C的坐标代入得出方程组,求出m和b的值,即可得出直线PC的表达式;
(2)根据对称的性质求出P′E′=PE=2
,CE′=CE=5+1=6,求出OE′,即可得出P′的坐标.
| 3 |
| 3 |
| 3 |
| 3 |
代入y=
| k |
| x |
(2)根据对称的性质求出P′E′=PE=2
| 3 |
解答: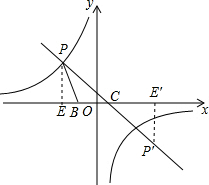 解:(1)如图,过P作PE⊥x轴于E,
解:(1)如图,过P作PE⊥x轴于E,
设BE=a,
∵B在PC的垂直平分线上,
∴PB=BC=4,
∴∠PCB=∠BPC=30°,
∴∠PBE=30°+30°=60°,
∴∠EPB=30°,
∴PE=
BE=
a,
a+4=
PE,
∴a+4=
×
a,
解得:a=2,
OE=2+(4-1)=5,PE=
a=2
即P的坐标是(-5,2
),
代入y=
得:k=-10
,
∴反比例函数的表达式是y=-
,
设直线PC的解析式是y=mx+b
把P、C的坐标代入得:
,
解得:m=-
,b=
,
∴直线PC的表达式是y=-
x+
.
(2)过P′作P′E′⊥x轴于E′,
∵根据对称的性质P′E′=PE=2
,CE′=CE=5+1=6,
∴OE′=6+1=7
P′的坐标是(7,-2
).
 解:(1)如图,过P作PE⊥x轴于E,
解:(1)如图,过P作PE⊥x轴于E,设BE=a,
∵B在PC的垂直平分线上,
∴PB=BC=4,
∴∠PCB=∠BPC=30°,
∴∠PBE=30°+30°=60°,
∴∠EPB=30°,
∴PE=
| 3 |
| 3 |
a+4=
| 3 |
∴a+4=
| 3 |
| 3 |
解得:a=2,
OE=2+(4-1)=5,PE=
| 3 |
| 3 |
即P的坐标是(-5,2
| 3 |
代入y=
| k |
| x |
| 3 |
∴反比例函数的表达式是y=-
10
| ||
| x |
设直线PC的解析式是y=mx+b
把P、C的坐标代入得:
|
解得:m=-
| ||
| 3 |
| ||
| 3 |
∴直线PC的表达式是y=-
| ||
| 3 |
| ||
| 3 |
(2)过P′作P′E′⊥x轴于E′,
∵根据对称的性质P′E′=PE=2
| 3 |
∴OE′=6+1=7
P′的坐标是(7,-2
| 3 |
点评:本题考查了对称性质、用待定系数法求出一次函数与反比例函数的解析式,含30度角的直角三角形性质,解二元一次方程组等知识点,本题题型比较好,综合性比较好,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是