题目内容
5.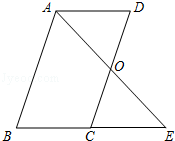 已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=45°和∠AEB=45°时,四边形ACED是正方形?请说明理由.
分析 (1)首先根据O是CD的中点,可得DO=CO,再证明∠D=∠OCE,然后可利用ASA定理证明△AOD≌△EOC;
(2)当∠B=45°和∠AEB=45°时,四边形ACED是正方形;首先证明∠BAE=90°,然后证明AC是BE边上的中线,根据直角三角形的性质可得AC=CE,然后利用等腰三角形的性质证明AC⊥BE,可得结论.
解答 (1)证明:∵O是CD的中点,
∴DO=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中$\left\{\begin{array}{l}{∠D=∠OCE}\\{DO=CO}\\{∠AOD=∠COE}\end{array}\right.$,
∴△AOD≌△EOC(ASA);
(2)解:当∠B=45°和∠AEB=45°时,四边形ACED是正方形,
∵∠B=45°和∠AEB=45°,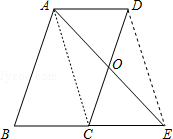
∴∠BAE=90°,
∵△AOD≌△EOC,
∴AO=EO,
∵DO=CO,
∴四边形ACED是平行四边形,
∴AD=CE,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴BC=CE,
∵∠BAE=90°,
∴AC=CE,
∴平行四边形ACED是菱形,
∵∠B=∠AEB,BC=CE,
∴AC⊥BE,
∴四边形ACED是正方形.
故答案为:45,45.
点评 此题主要考查了全等三角形的判定与性质,以及正方形的判定,关键是掌握邻边相等的矩形是正方形.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
10.菱形的两条对角线长分别为6和8,则菱形的面积是( )
| A. | 10 | B. | 20 | C. | 24 | D. | 48 |
14.若分式$\frac{x+1}{x+2}$的值为0,则x的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
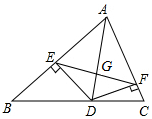 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,连接EF,EF与AD相交于点G.
如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,连接EF,EF与AD相交于点G.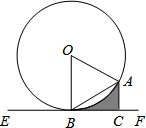 如图,⊙O的半径OA=2,AB是弦,直线EF经过点B,AC⊥EF于点C,∠BAC=∠OAB.
如图,⊙O的半径OA=2,AB是弦,直线EF经过点B,AC⊥EF于点C,∠BAC=∠OAB.