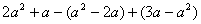题目内容
已知a,b,c为有理数,且a+b+c=0,a≥﹣b>|c|,则a,b,c三个数的符号是( )
A.a>0,b<0,c<0 B.a>0,b<0,c>0 C.a<0,b>0,c≥0 D.a>0,b<0,c≤0
D【考点】有理数大小比较.
【专题】推理填空题;实数.
【分析】首先根据a≥﹣b>|c|≥0,可得a>|c|,﹣b>|c|,所以a>0,﹣b>0,据此推得a>0,b<0;然后根据a≥﹣b,可得a+b≥0,再根据a+b+c=0,可得c≤0,据此解答即可.
【解答】解:∵a≥﹣b>|c|≥0,
∴a>|c|,﹣b>|c|,
∴a>0,﹣b>0,
∴a>0,b<0;
∵a≥﹣b,
∴a+b≥0,
又∵a+b+c=0,
∴c≤0,
∴a>0,b<0,c≤0.
故选:D.
【点评】(1)此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
(2)解答此题的关键是根据a≥﹣b>|c|,推得a>|c|,﹣b>|c|,进而判断出a>0,b<0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
小明根据柸州市出租车的收费标准,制定了打车费计算的数值转换机示意图:

(1)根据数值转换机程序计算下列乘客应付打车费用:
| 乘客 | 甲 | 乙 | 丙 | 丁 | 戍 |
| 输入/公里 | 1.5 | 2 | 4 | 6 | 8 |
| 输出/元 | __________ | __________ | __________ | __________ | __________ |
(2)通过填写表格,用一句话描述你的发现:__________
(3)请用代数式表示上述数值转换程序.

 __________
__________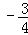 .
.