题目内容
10.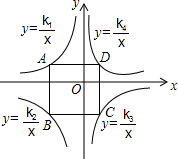 如图,边长为4的正方形ABCD的四个顶点分别在y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$,y=$\frac{{k}_{4}}{x}$上,且AB与y轴平行,则k1-k2+k3-k4的值为-16.
如图,边长为4的正方形ABCD的四个顶点分别在y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$,y=$\frac{{k}_{4}}{x}$上,且AB与y轴平行,则k1-k2+k3-k4的值为-16.
分析 如图,根据反比例函数k的几何意义得到S矩形AEOH=|k1|=-k1,S矩形BEOF=|k2|=k2,S矩形CGOF=|k3|=-k3,S矩形DGOH=|k4|=k4,然后利用正方形的面积得到-k1+k2-k3+k4=4×4=16,再变形代数式即可.
解答 解: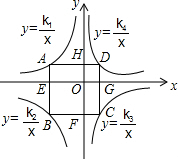 如图,
如图,
∵S矩形AEOH=|k1|=-k1,S矩形BEOF=|k2|=k2,S矩形CGOF=|k3|=-k3,S矩形DGOH=|k4|=k4,
∴-k1+k2-k3+k4=4×4=16,
∴k1-k2+k3-k4=-16.
故答案为-16.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了反比例函数k的几何意义.

练习册系列答案
相关题目
1.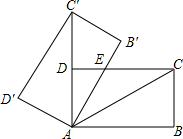 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )| A. | 3 | B. | 1.5 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
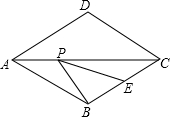 如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为$\sqrt{3}$+1.
如图,菱形ABCD的边长为2,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为$\sqrt{3}$+1.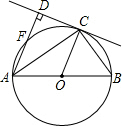 如图,AB为⊙O的直径,OC为⊙O的半径,AD⊥DC于D,AC平分∠DAB,AD交⊙O于点E.
如图,AB为⊙O的直径,OC为⊙O的半径,AD⊥DC于D,AC平分∠DAB,AD交⊙O于点E.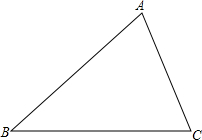 尺规作图:(不写作法,保留作图痕迹)
尺规作图:(不写作法,保留作图痕迹)