题目内容
在等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN过点A且MN∥BC.以点B为一锐角顶点作Rt△BDE,∠BDE=90°,且点D在直线MN上(不与点A重合).如图1,DE与AC交于点P,易证:BD=DP.(无需写证明过程)
(1)在图2中,DE与CA延长线交于点P,BD=DP是否成立?如果成立,请给予
证明,如果不成立,请说明理由;
(2)在图3中,DE与AC延长线交于点P,BD与DP是否相等?请直接写出你的结论,无需证明.
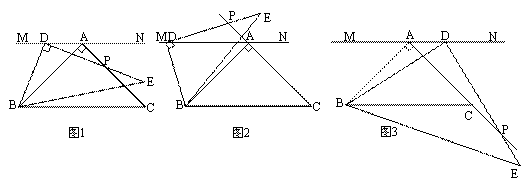
解:(1)在图2中BD=DP成立
证明:过点D作DF⊥AD交AB延长线于点F.
∵AD∥BC,∠ABC=45°
∴∠BAD=∠PAD=45°
∴△ADF是等腰直角三角形
∴AD=DF,∠F=45°
∵∠BDP=∠ADF=90°
∴∠ADP =∠FDB
∴△ADP≌△FDB
∴DP =BD
(2)图3中BD=DP

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
如图,已知l1∥l2,∠A=40°,∠1=60°,则∠2的度数为( )

|
| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
从1、2、3、4中任取两个不同的数,其乘积大于4的概率是( )
|
| A. |
| B. |
| C. |
| D. |
|


 ,则
,则 的值为______.
的值为______. ,其中x=1.
,其中x=1.



 B.
B.  C.
C.  D. 1
D. 1