题目内容
已知∠A0B=90°,OM平分∠AOB,在∠AOB的外部由点O引出两条射线OC、OD,若∠COD=150°,∠COM:∠DOM=3:2,则∠COB= .
考点:角的计算,角平分线的定义
专题:
分析:作出图形,根据题意可以求得∠COM的值,再分类讨论与OC相邻射线是OA还是OB,即可求得∠BOC的值;
解答:解:作出图形,
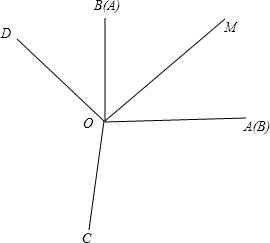
①射线OC和射线OB相邻
∵∠COM:∠DOM=3:2,∠COD=150°,
∴∠COM=126°,
∵∠AOM=∠BOM=45°,
∴∠BOC=126°-45°=81°,
②射线OC和射线OA相邻,
∵∠COM:∠DOM=3:2,∠COD=150°,
∴∠COM=126°,
∵∠AOM=∠BOM=45°,
∴∠AOC=126°-45°=81°,
∴∠BOC=81°+90°=171°.
③∠AOB是在∠COD内部,
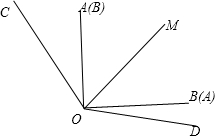
∵∠COM:∠DOM=3:2,∠COD=150°,
∴∠COM=90°,
∵∠AOM=∠BOM=45°,
∴∠AOC=45°或135°,
故答案为 81°或171°或45°或135°.

①射线OC和射线OB相邻
∵∠COM:∠DOM=3:2,∠COD=150°,
∴∠COM=126°,
∵∠AOM=∠BOM=45°,
∴∠BOC=126°-45°=81°,
②射线OC和射线OA相邻,
∵∠COM:∠DOM=3:2,∠COD=150°,
∴∠COM=126°,
∵∠AOM=∠BOM=45°,
∴∠AOC=126°-45°=81°,
∴∠BOC=81°+90°=171°.
③∠AOB是在∠COD内部,

∵∠COM:∠DOM=3:2,∠COD=150°,
∴∠COM=90°,
∵∠AOM=∠BOM=45°,
∴∠AOC=45°或135°,
故答案为 81°或171°或45°或135°.
点评:本题考查了角的和与差的计算,解本题的关键是分类讨论与OC相邻射线是OA还是OB.

练习册系列答案
相关题目
下列运算正确的是( )
| A、x2•x3=x5 |
| B、x2+x2=2x4 |
| C、(-2x2)4=16x6 |
| D、(x+3y)(x-3y)=x2-3y2 |
 如图,能和∠α构成内错角的角的个数是( )
如图,能和∠α构成内错角的角的个数是( )| A、1 | B、2 | C、3 | D、4 |
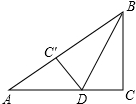 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′处,那么CD=( )
如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′处,那么CD=( )