题目内容
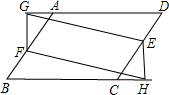 如图,在平行四边形ABCD中,E、F分别在CD、AB上,且AF=CE,FG⊥AD于G,EH⊥BC于H,求证:四边形EGFH是平行四边形.
如图,在平行四边形ABCD中,E、F分别在CD、AB上,且AF=CE,FG⊥AD于G,EH⊥BC于H,求证:四边形EGFH是平行四边形.考点:平行四边形的判定与性质
专题:证明题
分析:首先证明△AGF≌△CHE,即可证得FG=EH,根据一组对边平行且相等的四边形是平行四边形即可证得.
解答:证明:∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,
∴∠GAF=∠HCE,
在△AGF和△CHE中,
,
∴△AGF≌△CHE,
∴FG=EH,
又∵FG⊥AD于G,EH⊥BC,平行四边形ABCD中,AD∥BC,
∴FG∥EH,
∴四边形EGFH是平行四边形.
∴∠BAD=∠BCD,
∴∠GAF=∠HCE,
在△AGF和△CHE中,
|
∴△AGF≌△CHE,
∴FG=EH,
又∵FG⊥AD于G,EH⊥BC,平行四边形ABCD中,AD∥BC,
∴FG∥EH,
∴四边形EGFH是平行四边形.
点评:本题考查了全等三角形的判定与性质,以及平行四边形的判定,平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
相关题目
下列实数中,无理数是( )
| A、2 | ||
| B、-1 | ||
C、
| ||
D、
|
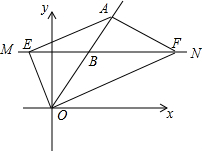 如图,在平面直角坐标系中,点A是动点且纵坐标为6,点B是线段OA上一动点,过点B作直线MN∥x轴,设MN分别交射线OA与x轴所成的两个角的平分线于点E、F.
如图,在平面直角坐标系中,点A是动点且纵坐标为6,点B是线段OA上一动点,过点B作直线MN∥x轴,设MN分别交射线OA与x轴所成的两个角的平分线于点E、F.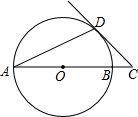 如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°.
如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°.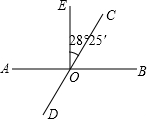 如图,已知直线AB、CD相交于点O,OE平分∠AOB,∠EOC=28°25′.
如图,已知直线AB、CD相交于点O,OE平分∠AOB,∠EOC=28°25′.