题目内容
 如图,O是直线AB上一点,OC,OD,OE是三条射线,且OC平分∠AOD,∠BOE=2∠DOE,∠COE=80°,求∠BOE的度数.
如图,O是直线AB上一点,OC,OD,OE是三条射线,且OC平分∠AOD,∠BOE=2∠DOE,∠COE=80°,求∠BOE的度数.
解:设∠DOE=x,则∠BOE=2x,
∵∠BOD=∠BOE+∠EOD,∴∠BOD=3x.∴∠AOD=180°-∠BOD=180°-3x.
∵OC平分∠AOD,∴∠COD= ∠AOD=
∠AOD= (180°-3x)=90°-
(180°-3x)=90°-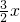 .
.
∵∠COE=∠COD+∠DOE=90°- x+x=90°-
x+x=90°- ,
,
由题意有90°- =80°,解得x=20°,即∠DOE=20°,
=80°,解得x=20°,即∠DOE=20°,
∴∠BOE=40°.
分析:设∠DOE=x,则∠BOE=2x,根据角之间的等量关系求出∠AOD、∠COD、∠COE的大小,然后解得x.
点评:本题主要考查角的计算的知识点,运用好角的平分线这一知识点是解答的关键,本题难度不大.
∵∠BOD=∠BOE+∠EOD,∴∠BOD=3x.∴∠AOD=180°-∠BOD=180°-3x.
∵OC平分∠AOD,∴∠COD=
 ∠AOD=
∠AOD= (180°-3x)=90°-
(180°-3x)=90°-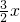 .
.∵∠COE=∠COD+∠DOE=90°-
 x+x=90°-
x+x=90°- ,
,由题意有90°-
 =80°,解得x=20°,即∠DOE=20°,
=80°,解得x=20°,即∠DOE=20°,∴∠BOE=40°.
分析:设∠DOE=x,则∠BOE=2x,根据角之间的等量关系求出∠AOD、∠COD、∠COE的大小,然后解得x.
点评:本题主要考查角的计算的知识点,运用好角的平分线这一知识点是解答的关键,本题难度不大.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
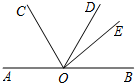 如图,O是直线AB上一点,OC,OD,OE是三条射线,且OC平分∠AOD,∠BOE=2∠DOE,∠COE=80°,求∠BOE的度数.
如图,O是直线AB上一点,OC,OD,OE是三条射线,且OC平分∠AOD,∠BOE=2∠DOE,∠COE=80°,求∠BOE的度数.
 如图,O是直线AB上一点,∠AOC=134°18′,求∠BOC的度数.
如图,O是直线AB上一点,∠AOC=134°18′,求∠BOC的度数. 如图,O是直线AB上的一点,∠AOC=53°17′,则∠BOC的度数是
如图,O是直线AB上的一点,∠AOC=53°17′,则∠BOC的度数是 如图,O是直线AB上任意一点,OC平分∠AOB.按下列要求画图并回答问题:
如图,O是直线AB上任意一点,OC平分∠AOB.按下列要求画图并回答问题: