题目内容
【题目】四边形![]() 内接于
内接于![]() ,连接
,连接![]() ,且
,且![]() .
.
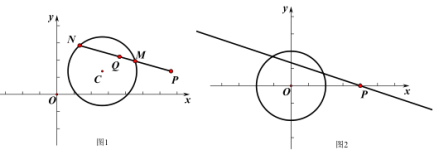
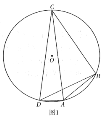
(1)如图1,求证:![]() ;
;
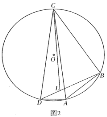
(2)如图2,点![]() 在
在![]() 上,连接
上,连接![]() ,求证:
,求证:![]() ;
;
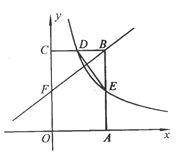
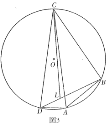
(3)如图3,在(2)的条件下,若![]() 的半径长为
的半径长为![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据圆周角性质和等腰三角形性质可得![]() ,
,![]() ,结合圆的内接四边形对角互补性质可得;
,结合圆的内接四边形对角互补性质可得;
(2)延长![]() 到
到![]() 使
使![]() ,连接
,连接![]() ,由(1)证
,由(1)证![]() ,
,![]() ,得
,得![]() ,
,![]() ,可进一步得
,可进一步得![]() ,
,
由![]() ,得
,得![]() ,再结合
,再结合![]() ,证
,证![]() ,可证出
,可证出![]() ;
;
(3)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,证
,证![]() ,得
,得![]() ,在
,在![]() 中,由勾股定理得,
中,由勾股定理得,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,由
,由![]() ,得
,得![]() ,求出
,求出![]() ,
,![]() ,
,![]() ,证
,证![]() ,得
,得![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,证
,证![]() ,根据
,根据![]() ,得
,得![]() ,化简得到
,化简得到![]() ,在
,在![]() 中,根据勾股定理得
中,根据勾股定理得![]() .
.
证明:(1)∵![]() ,∴
,∴![]() ,
,
∵![]() ,又∵
,又∵![]() ,
,
∴![]() ;
;
(2)延长![]() 到
到![]() 使
使![]() ,连接
,连接![]() ,
,
∵![]() ,
,
又∵![]() ,
,
∴![]() ,∵
,∵![]()
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ;
;
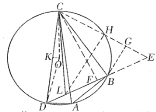
(3)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
设![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
在![]() 中,由勾股定理得,
中,由勾股定理得,![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
∴![]() (
(![]() 舍去),∴
舍去),∴![]() .
.

练习册系列答案
相关题目
【题目】二次函数![]() 上部分点的横坐标x与纵坐标y的对应值如下表:
上部分点的横坐标x与纵坐标y的对应值如下表:
x | … |
|
| 0 | 1 | 2 | 3 | … |
y | … | 3 |
| 0 |
| 0 | m | … |

(1)直接写出此二次函数的对称轴 ;
(2)求b的值;
(3)直接写出表中的m值,m= ;
(4)在平面直角坐标系xOy中,画出此二次函数的图象.