Question

【题目】如图，已知一次函数的图象交轴于点，交轴于点，点在轴正半轴上，点在射线上，且．垂直轴于点．

点坐标为________，点坐标为________．

操作：将一足够大的三角板的直角顶点放在射线或射线上，一直角边始终过点，另一直角边与轴相交于点．问是否存在这样的点，使以点，，为顶点的三角形与全等？若存在，求出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）（2）存在这样的点，使以点，，为顶点的三角形与全等

【解析】

（1）根据点E在x轴正半轴上，OE=OF=10，即可得出E（10，0），再根据点F在射线BA上，可设F（x，x+2），则OH=x，FH=x+2，最后根据勾股定理求得x即可；

（2）当点Q在射线HF上时，分两种情况：①QE=OE=10，②QP=OE=10；当点Q在射线AF上时，分两种情况：①QE=OE=10，②QP=OE=10，分别作辅助线构造直角三角形或相似三角形，求得QH的长，即可得出点Q的坐标．

（1）∵点E在x轴正半轴上，OE=OF=10，∴E（10，0）．

∵点F在射线BA上，∴可设F（x，x+2），则OH=x，FH=x+2，如图，连接OF，则

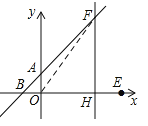
Rt△OHF中，x2+（x+2）2=102，解得：x=6，∴x+2=8，∴F（6，8）．

故答案为：（10，0），（6，8）；

（2）存在这样的点Q，使以点P，Q，E为顶点的三角形与△POE全等．

当点Q在射线HF上时，分两种情况：

①如图所示，若QE=OE=10，而HE=10﹣6=4，∴在Rt△QHE中，QH===2，∴Q（6，2）；

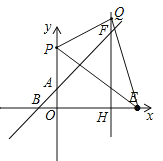
②如图所示，若QP=OE=10，作PK⊥FH于K，则∠PKQ=∠QHE=90°，QK==8．

∵∠PQK+∠EQH=∠QEH+∠EQH=90°，∴∠PQK=∠QEH，∴△PQK∽△QEH，∴=，即=，解得：QH=3，∴Q（6，3）；

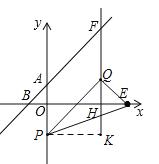
当点Q在射线AF上时，分两种情况：

①如图所示，若QE=OE=10，设Q（x，x+2），作QR⊥x轴于R，则RE=10﹣x，QR=x+2，∴Rt△QRE中，（10﹣x）2+（x+2）2=102，解得：x=4±，∴Q（4+，6+）或（4﹣，6﹣）；

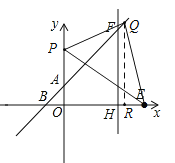
②如图所示，若QP=OE=10，则QE=OP，设Q（x，x+2）．

∵∠POE=90°，∴四边形OPQE是矩形，∴x=OE=10．

∵Q在射线AF上，∴x+2=QE=12，∴Q（10，12）．