题目内容
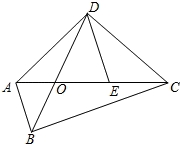
如图：四边形ABCD对角线AC与BD相交于点O，OD=2OA，OC=2OB．
（1）求证：△AOB∽△DOC；
（2）点E在线段OC上，若AB∥DE，求证：OD2=OE•OC．
【考点】相似三角形的判定与性质．
【专题】证明题．
【分析】（1）根据对应边成比例，夹角相等，可证△AOB∽△DOC；
（2）根据相似三角形的性质结合已知条件可得△DOC∽△EOD，再根据相似三角形对应边成比例求解．
【解答】证明：（1）∵OD=2OA，OC=2OB，
∴
．
又∠AOB=∠DOC，
∴△AOB∽△DOC．
（2）由（1）得：△AOB∽△DOC．
∴∠ABO=∠DCO．
∵AB∥DE，
∴∠ABO=∠EDO．
∴∠DCO=∠EDO．
∵∠DOC=∠EOD，
∴△DOC∽△EOD．
∴
．
∴OD2=OE•OC．
【点评】本题考查了相似三角形的判定与性质，三角形相似的判定和性质一直是中考考查的热点之一，注意找准对应角和对应边．
练习册系列答案
相关题目
=_ ___．
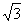≈1.732，
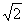≈1.414）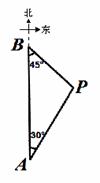
图，正△ABC中，P为BC上一点，D为AC上一点，∠APD=60°，BP=1，CD=
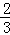，则△ABC的边长为__________．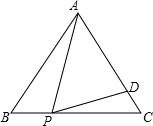
= 
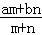元/kg．（混合单价=
）．
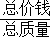m
36因式分解的结果是
，则
的值是
B.
C.
D.