题目内容
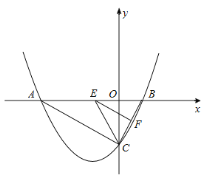
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 和
和![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点.
点.
(1)求此抛物线的解析式;
(2)设![]() 是线段
是线段![]() 上的动点,作
上的动点,作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,当
,当![]() 的面积是
的面积是![]() 面积的2倍时,求
面积的2倍时,求![]() 点的坐标;
点的坐标;
(3)若![]() 为抛物线上
为抛物线上![]() 、
、![]() 两点间的一个动点,过
两点间的一个动点,过![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于
于![]() ,当
,当![]() 点运动到什么位置时,线段
点运动到什么位置时,线段![]() 的值最大,并求此时
的值最大,并求此时![]() 点的坐标.
点的坐标.

【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)当
;(3)当![]() 点的坐标为
点的坐标为![]() 时,线段
时,线段![]() 取最大值.
取最大值.
【解析】
(1)将A、B的坐标代入抛物线的解析式中,求出系数的值,即可求得抛物线的解析式;
(2)△CEF和△BEF同高,则面积比等于底边比,由此可得出CF=2BF;易证得△BEF∽△BAC,根据相似三角形的性质,即可求得BE、AB的比例关系,由此可求出E点坐标;
(3)PQ的长实际是直线AC与抛物线的函数值的差,可设P点横坐标为a,用a表示出P、Q的纵坐标,然后可得出PQ的长与a的函数关系式,根据所得函数的性质即可求出PQ最大时a的值,也就能求出此时P点的坐标.
解:(1)将点![]() ,
,![]() 坐标代入抛物线解析式得:
坐标代入抛物线解析式得:
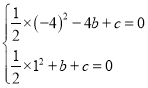 ,
,
解得: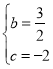 ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
(2)如图,![]() ,
,
![]() ,则
,则![]() .
.
![]() ,
,
∴![]() ,
,
![]() ,
,
∵![]() 、
、![]() ,
,
则![]() ,
,
∴![]() .
.
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
(3)∵抛物线的解析式为![]() ,
,
当x=0时,y=2,则![]() ,
,
设直线AC的解析式为:![]() ,分别代入
,分别代入![]() 、
、![]() 得:
得:
![]() ,解得:
,解得: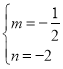 ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
设![]() 点的坐标为
点的坐标为![]() ,
,
![]() 点是过点
点是过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 的交点,则
的交点,则![]() 点的坐标为
点的坐标为![]() .则有:
.则有:
![]()
![]() ,
,
即当![]() 时,线段
时,线段![]() 取最大值,
取最大值,
此时![]() 点的坐标为
点的坐标为![]() .
.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目