题目内容
 如图,△ABC中,∠ABC=90°,如果AB=AD,CE=CB,那么∠EBD=( )
如图,△ABC中,∠ABC=90°,如果AB=AD,CE=CB,那么∠EBD=( )| A、30° | B、45° |
| C、50° | D、60° |
考点:等腰三角形的性质
专题:
分析:首先∠A=x°,根据∠ABC=90°得到∠C=(90-x)°,利用AB=AD,CE=CB,得到∠ABD=∠ADB,∠BEC=∠EBC,从而得到∠ADB=
°=(90-
)°、
∠EBC=[180-(90-x)]÷2=[45+
]°,利用∠EBD=∠EBC-∠DBC=(45+
)°-
°=45°求解即可.
| 180-x |
| 2 |
| x |
| 2 |
∠EBC=[180-(90-x)]÷2=[45+
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
解答:解设∠A=x°,
∵∠ABC=90°,
∴∠C=(90-x)°,
∵AB=AD,CE=CB,
∴∠ABD=∠ADB,∠BEC=∠EBC,
∴∠ADB=
°=(90-
)°,∠EBC=[180-(90-x)]÷2=[45+
]°,
∴∠DBC=∠ADB-∠C=(90-
)°-(90-x)°=
°,
∴∠EBD=∠EBC-∠DBC=(45+
)°-
°=45°,
故选B.
∵∠ABC=90°,
∴∠C=(90-x)°,
∵AB=AD,CE=CB,
∴∠ABD=∠ADB,∠BEC=∠EBC,
∴∠ADB=
| 180-x |
| 2 |
| x |
| 2 |
| x |
| 2 |
∴∠DBC=∠ADB-∠C=(90-
| x |
| 2 |
| x |
| 2 |
∴∠EBD=∠EBC-∠DBC=(45+
| x |
| 2 |
| x |
| 2 |
故选B.
点评:本题考查了等腰三角形的性质,解题过程中用到了方程的数学思想,中考中应用很多.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
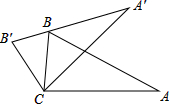 如图,将△ABC绕顶点C逆时针旋转得到△A′B′C′,且点B刚好落在A′B′上,若∠A=25°,∠BCA′=45°,则∠A′BA等于( )
如图,将△ABC绕顶点C逆时针旋转得到△A′B′C′,且点B刚好落在A′B′上,若∠A=25°,∠BCA′=45°,则∠A′BA等于( )| A、30° | B、35° |
| C、40° | D、45° |
 如图,在平面直角坐标系中,三角形的顶点都在格点上,△BDE是由△ABC绕着某点逆时针旋转一定的角度得到的,则该点的坐标为
如图,在平面直角坐标系中,三角形的顶点都在格点上,△BDE是由△ABC绕着某点逆时针旋转一定的角度得到的,则该点的坐标为 如图:每个小方格都是边长为1的正方形,以O点为坐标原点,建立平面直角坐标系.
如图:每个小方格都是边长为1的正方形,以O点为坐标原点,建立平面直角坐标系.


