题目内容
如图，在平行四边形
中，
为
的中点，连接
并延长交
的延长线于点
．
(1)求证：
；
(2)当与
满足什么数量关系时，四边形
是矩形，并说明理由．
中，为的中点，连接并延长交的延长线于点．(1)求证：
；(2)当
与满足什么数量关系时，四边形是矩形，并说明理由．(1)证明：∵四边形是平行四边形
∴
∴
∵为的中点
∴
∴
∴.
(2)解:当
时,四边形是矩形.理由如下: ∵
∴四边形是平行四边形
∵
∴四边形是矩形.
是平行四边形∴
∴
∵
为的中点∴
∴
∴
.(2)解:当
时,四边形是矩形.理由如下: ∵∴四边形
是平行四边形∵
∴四边形
是矩形.（1）根据平行四边形的性质得到两角一边对应相等，利用AAS判定△ABE≌△FCE，从而得到AB=CF；
（2）由已知可得四边形ABFC是平行四边形，BC=AF，根据对角线相等的平行四边形是矩形，可得到四边形ABFC是矩形．
（2）由已知可得四边形ABFC是平行四边形，BC=AF，根据对角线相等的平行四边形是矩形，可得到四边形ABFC是矩形．
练习册系列答案
相关题目
比
大
.设
,
，那么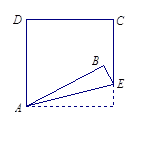
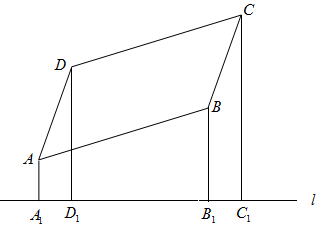
及四边形外一直线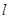
，四个顶点
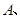
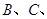
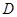到直线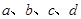
．
的周长是18cm，
<
.对角线
、
相交于点
,若
与
的周长差是5cm，则边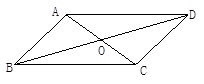
，BC=26
的速度运动，动点Q从点C开始沿CB以3
，问
为何值时，（1）四边形PQCD是平行四边形．（2）当
中，
，
，
，
，则
（ ）
