题目内容
（1999•贵阳）如图，已知圆心角∠BOC=80°，那么圆周角∠BAC= 度．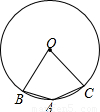
【答案】分析：在优弧BC上任取一点D（不与B、C重合），连接BD、CD；由圆周角定理，求得∠BDC的度数；而四边形ABDC是⊙O的内接四边形，则内对角∠BDC、∠BAC互补，由此得解．
解答：
解：如图；在优弧BC上取一点D，连接BD、CD；
由圆周角定理，得：∠BDC=
∠BOC=40°；
∵四边形ABDC内接于⊙O，
∴∠BAC+∠BDC=180°；
∴∠BAC=180°-∠BDC=140°．
点评：此题主要考查的是圆周角定理及圆内接四边形的性质．
解答：
解：如图；在优弧BC上取一点D，连接BD、CD；由圆周角定理，得：∠BDC=
∠BOC=40°；∵四边形ABDC内接于⊙O，
∴∠BAC+∠BDC=180°；
∴∠BAC=180°-∠BDC=140°．
点评：此题主要考查的是圆周角定理及圆内接四边形的性质．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
