题目内容
若k=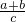 =
=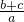 =
=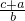 ,则一次函数y=(2-k)x+1一定不经过
,则一次函数y=(2-k)x+1一定不经过
- A.第一象限
- B.第二象限
- C.第三象限
- D.第四象限
D
分析:根据比例的性质求得a+b=ck ①,b+c=ak ②,c+a=bk ③;由①②③求得2(a+b+c)=k(a+b+c);然后分两种情况讨论(当a+b+c≠0和当a+b+c=0)来求k值;最后根据一次函数图象的性质作出选择.
解答:根据已知条件,得出
a+b=ck ①,
b+c=ak ②,
c+a=bk ③,
①+②+③,得 2(a+b+c)=k(a+b+c).
(1)当a+b+c≠0,则k=2;
(2)当a+b+c=0,则a+b=-c,b+c=-a,a+c=-b,
∴k=-1;
∵y=(2-k)x+1为一次函数,所以2-k≠0,即k≠2,
∴k=-1;
∴y=3x+1经过一、二、三象限,一定不过第四象限.
故选D.
点评:本题考查了比例的性质、一次函数的性质.直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限.k<0时,直线必经过二、四象限.b>0时,直线与y轴正半轴相交.b=0时,直线过原点;b<0时,直线与y轴负半轴相交.
分析:根据比例的性质求得a+b=ck ①,b+c=ak ②,c+a=bk ③;由①②③求得2(a+b+c)=k(a+b+c);然后分两种情况讨论(当a+b+c≠0和当a+b+c=0)来求k值;最后根据一次函数图象的性质作出选择.
解答:根据已知条件,得出
a+b=ck ①,
b+c=ak ②,
c+a=bk ③,
①+②+③,得 2(a+b+c)=k(a+b+c).
(1)当a+b+c≠0,则k=2;
(2)当a+b+c=0,则a+b=-c,b+c=-a,a+c=-b,
∴k=-1;
∵y=(2-k)x+1为一次函数,所以2-k≠0,即k≠2,
∴k=-1;
∴y=3x+1经过一、二、三象限,一定不过第四象限.
故选D.
点评:本题考查了比例的性质、一次函数的性质.直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限.k<0时,直线必经过二、四象限.b>0时,直线与y轴正半轴相交.b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 (2012•北辰区一模)在-3≤x≤0范围内,二次函数
(2012•北辰区一模)在-3≤x≤0范围内,二次函数 时,函数值的范围为
时,函数值的范围为 ,则此一次函的解析式为( )
,则此一次函的解析式为( )