题目内容
O是正方形ABCD内一点,若△OAD是正三角形,则∠DCO=________.
75°
分析:根据正方形的四条边都相等以及等边三角形的三条边都相等可得OD=CD,再根据正方形的角都是直角,等边三角形的角都是60°,求出∠CDO=30°,然后利用三角形的内角和定理列式计算即可得解.
解答: 解:如图,∵四边形ABCD是正方形,
解:如图,∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∵△OAD是正三角形,
∴OD=AD,∠ADO=60°,
∴OD=CD,∠CDO=90°-60°=30°,
∴∠DOC=∠DCO(等边对等角),
在△OCD中,∠DCO= (180°-30°)=75°.
(180°-30°)=75°.
故答案为:75°.
点评:本题考查了正方形的性质,等边三角形的性质,求出△OCD是顶角为30°的等腰三角形是解题的关键.
分析:根据正方形的四条边都相等以及等边三角形的三条边都相等可得OD=CD,再根据正方形的角都是直角,等边三角形的角都是60°,求出∠CDO=30°,然后利用三角形的内角和定理列式计算即可得解.
解答:
 解:如图,∵四边形ABCD是正方形,
解:如图,∵四边形ABCD是正方形,∴AD=CD,∠ADC=90°,
∵△OAD是正三角形,
∴OD=AD,∠ADO=60°,
∴OD=CD,∠CDO=90°-60°=30°,
∴∠DOC=∠DCO(等边对等角),
在△OCD中,∠DCO=
 (180°-30°)=75°.
(180°-30°)=75°.故答案为:75°.
点评:本题考查了正方形的性质,等边三角形的性质,求出△OCD是顶角为30°的等腰三角形是解题的关键.

练习册系列答案
相关题目
 如图,点P是正方形ABCD内的一点,若PA=a,PB=2a,PC=3a,(a>0),那么∠APB的大小是( )
如图,点P是正方形ABCD内的一点,若PA=a,PB=2a,PC=3a,(a>0),那么∠APB的大小是( )| A、100° | B、120° | C、135° | D、150° |
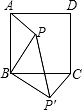 如图,P是正方形ABCD内一点,将△ABP移到△CBP′位置,若BP=3,则PP′的长为
如图,P是正方形ABCD内一点,将△ABP移到△CBP′位置,若BP=3,则PP′的长为 已知:如图,P是正方形ABCD内一点,∠APB=135°,BP=1,AP=
已知:如图,P是正方形ABCD内一点,∠APB=135°,BP=1,AP= B与BC重合,连接PP′,得到△PBP′.
B与BC重合,连接PP′,得到△PBP′. 如图,点P是正方形ABCD内一点,连接AP、BP、CP、DP,若△ABP是等边三角形.
如图,点P是正方形ABCD内一点,连接AP、BP、CP、DP,若△ABP是等边三角形.