题目内容
13. 如图,一艘轮船位于灯塔B的正西方向A处,且A处与灯塔B相距60海里,轮船沿东北方向匀速前行,到达位于灯塔B的北偏东15°方向上的C处.
如图,一艘轮船位于灯塔B的正西方向A处,且A处与灯塔B相距60海里,轮船沿东北方向匀速前行,到达位于灯塔B的北偏东15°方向上的C处.(1)求∠ACB的度数;
(2)求灯塔B到C处的距离.(结果保留根号)
分析 (1)利用三角形内角和定理进行计算;
(2)过点B作AC的垂线,垂足为D.在△BDC中利用三角函数即可求解.
解答  解:(1)在△ABC中,∠CAB=45°,∠CBA=90°+15°=105°.则∠ACB=180°-45°-105°=30°,即∠ACB=30°;
解:(1)在△ABC中,∠CAB=45°,∠CBA=90°+15°=105°.则∠ACB=180°-45°-105°=30°,即∠ACB=30°;
(2)过点B作AC的垂线,垂足为D,依题意可得∠DAB=45°,∠DBA=45°,AB=60海里.
在△BDC中,∠DBC=45°+15°=60°,∠BDC=90°,cos∠DBC=$\frac{BD}{BC}$=$\frac{30\sqrt{2}}{BC}$=cos60°=$\frac{1}{2}$.
∴BC=60$\sqrt{2}$(海里).
答:灯塔B到C处的距离是60$\sqrt{2}$海里.
点评 本题主要考查了方向角含义,正确记忆三角函数的定义是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列方程中是二元一次方程的是( )
| A. | 2x+y=6 | B. | y2+x=1 | C. | x2+3x+5=0 | D. | $\frac{2}{x}$+x2+1=0 |

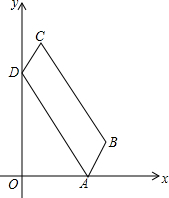 如图,在?ABCD中,∠BAD=60°,点A在x轴的正半轴上,点D在y轴的正半轴上,tan∠OAD=$\sqrt{3}$,AD和DC的长分别是方程x2-8x+12=0的两个根(AD>DC).
如图,在?ABCD中,∠BAD=60°,点A在x轴的正半轴上,点D在y轴的正半轴上,tan∠OAD=$\sqrt{3}$,AD和DC的长分别是方程x2-8x+12=0的两个根(AD>DC).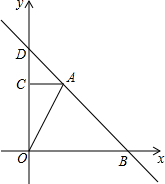 综合与探究:如图,在平面直角坐标系中,Rt△AOC的直角边OC在y轴正半轴上,且顶点O与坐标原点重合,点A的坐标为(2,4),直线y=-x+b过点A,与x轴交于点B.
综合与探究:如图,在平面直角坐标系中,Rt△AOC的直角边OC在y轴正半轴上,且顶点O与坐标原点重合,点A的坐标为(2,4),直线y=-x+b过点A,与x轴交于点B.