Question

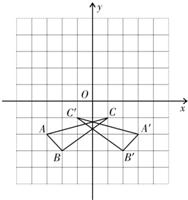如图，△ABC是格点三角形．且A（-3，-2），B（-2，-3），C（1，-1）．
（1）请在图中画出△ABC关于y轴的对称△A′B′C′；
（2）写出△A′B′C′各点坐标．并计算△A′B′C′的面积．

Answer 1

分析：（1）从三角形的各点向对称轴引垂线并延长相同单位得到各点的对应点，顺次连接即可．
（2）从图上读出各点的坐标，利用勾股定理计算出三角形的底和高，根据面积公式计算．

解答：解：（1）△ABC关于y轴的对称△A′B′C′如图所示．

（2）由图可知：A′（3，-2），B′（2，-3），C′（-1，-1），（4分）
S_△ABC=4×2-

1

2

×4×1-

1

2

×1×1-

1

2

×3×2=2

1

2

（面积单位）．（6分）

点评：本题综合考查了轴对称变换及坐标系的应用．