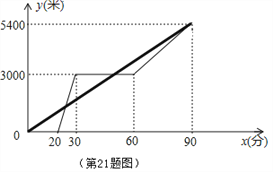
题目内容
【题目】某电视厂要印刷产品宣传材料，甲印刷厂提出：每份材料收
元印刷费，另收
元制版费，乙厂提出：每份材料收
元印刷费，不收制版费．
（1）分别写出两厂的收费
（元）与印制数量
（份）之间的函数解析式；
（2）电视机厂拟拿出
元用于印刷宣传材料，找哪家印刷厂印刷的宣传材料能多一些？
（3）印刷数量在什么范围时，在甲厂印刷合算？
【答案】（1）
；
；（2）甲厂印制的宣传材料多一些；（3）当印制数量大于
份时，在甲厂印刷合算．
【解析】
（1）直接根据题意列出函数解析式即可；
（2）把y=3000分别代入（1）中所求的函数关系式中求出x的值，比较大小即可；
（3）根据“甲厂的费用＜乙厂的费用”列出不等式x+1000＜2x求解即可．
（1）甲厂的收费
（元）与印刷数量
（份）之间的函数解析式为：
；
乙厂的收费（元）与印刷数量（份）之间的函数解析式为：
；
（2）根据题意可知，若找甲厂印刷，设可以印制份，则：
，
解得：
；
若找乙厂印刷，设可以印制份，则：
，
解得：
．
所以，甲厂印制的宣传材料多一些；
（3）设印刷份时，在甲厂印刷合算．
根据题意可得：
，
解得：
．
∴ 当印制数量大于
份时，在甲厂印刷合算．
【题目】如图，已知直线
与双曲线y＝
交于A、B两点，点B的坐标为(-4，-2)，C为第一象限内双曲线y＝
上一点，且点C在直线
的上方．
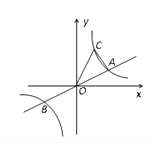
(1)求双曲线的函数解析式；
(2)若△AOC的面积为6，求点C的坐标．
【题目】列方程式应用题．
天河食品公司收购了200吨新鲜柿子，保质期15天，该公司有两种加工技术，一种是加工为普通柿饼，另一种是加工为特级霜降柿饼，也可以不需加工直接销售．相关信息见表：
品种 | 每天可加工数量（吨） | 每吨获利（元） |
新鲜柿子 | 不需加工 | 1000元 |
普通柿饼 | 16吨 | 5000元 |
特级霜降柿饼 | 8吨 | 8000元 |
由于生产条件的限制，两种加工方式不能同时进行，为此公司研制了两种可行方案：
方案1：尽可能多地生产为特级霜降柿饼，没来得及加工的新鲜柿子，在市场上直接销售；
方案2：先将部分新鲜柿子加工为特级霜降柿饼，再将剩余的新鲜柿子加工为普通柿饼，恰好15天完成．
请问：哪种方案获利更多？获利多少元？
