题目内容
 如图所示,⊙O是△ABC的外接圆.若∠ACB=35°,则∠OBA的度数等于
如图所示,⊙O是△ABC的外接圆.若∠ACB=35°,则∠OBA的度数等于
- A.35°
- B.55°
- C.70°
- D.110°
B
分析:由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠AOB的度数,又由OA=OB,根据等边对等角与三角形内角和定理,即可求得答案.
解答:∵∠ACB=35°,
∴∠AOB=2∠ACB=70°,
∵OA=OB,
∴∠OBA=∠OAB= =55°.
=55°.
故选B.
点评:此题考查了圆周角定理、等腰三角形的性质以及三角形内角和定理.此题难度不大,注意掌握数形结合思想的应用是解此题的关键.
分析:由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠AOB的度数,又由OA=OB,根据等边对等角与三角形内角和定理,即可求得答案.
解答:∵∠ACB=35°,
∴∠AOB=2∠ACB=70°,
∵OA=OB,
∴∠OBA=∠OAB=
 =55°.
=55°.故选B.
点评:此题考查了圆周角定理、等腰三角形的性质以及三角形内角和定理.此题难度不大,注意掌握数形结合思想的应用是解此题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 24、如图所示,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:∠ADC=∠BDE.
24、如图所示,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:∠ADC=∠BDE. 46、如图所示,AB是直径,D是圆上任意一点,C不与A、B重合,连接BD,并延长得到C,使DC=DB,连接AC,判断△ABC形状.并说明理由.
46、如图所示,AB是直径,D是圆上任意一点,C不与A、B重合,连接BD,并延长得到C,使DC=DB,连接AC,判断△ABC形状.并说明理由.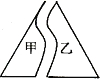 如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是
如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是 如图所示,AD是△ABC的中线,DF⊥AC,DE⊥AB,垂足分别为F,E,BE=CF.求证:AD平分∠BAC.
如图所示,AD是△ABC的中线,DF⊥AC,DE⊥AB,垂足分别为F,E,BE=CF.求证:AD平分∠BAC.